Integral Substitusi dan Parsial

Intergral substitusi dan parsial merupakan metode yang bisa kamu gunakan dalam menyelesaikan permasalahan integral itu sendiri. Integral substitusi yaitu metode yang digunakan pada persoalan integral dimana pada bagian fungsi adalah turunan dari fungsi yang lainnya.

Sedangkan integral parsial digunakan ke dalam persoalan integral yang lebih kompleks. Biasanya, integral parsial akan digunakan ketika rumus atau metode yang tersedia sudah tidak bisa lagi digunakan.

Mau tahu lebih lanjut mengenai jenis integral tersebut? Berikut ini materi selengkapnya untuk kamu.

A. Integral Substitusi

1. Integral Substitusi Pada Fungsi Aljabar

Ciri-ciri soal yang bisa diselesaikan dengan rumus integral substitusi ialah memiliki faktor turunan dari faktor lainnya. Sedangkan teknik integral substitusi pada fungsi aljabar yaitu f(x) bisa diubah dalam bentuk k.(g(x))ⁿ.g^I(x).

Perhatikan jika U= g(x) maka(x) atau dU= g^I(x) .dx

Jika Maka integral tersebut bisa diselesaikan dengan memisalkan U= g(x) serta U= g^I(x) dx sehingga akan diperoleh persamaan sebagai berikut:

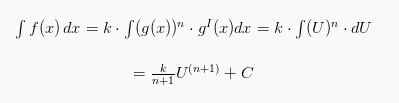
Hal tersebut berlaku dengan n ≠–1.

Namun apabilan n = -1, sehingga akan diperoleh:

. dU = 1n U + C

Contohnya yaitu:

Jika f(x) = (x⁴+5)³x³, untuk memperoleh integralnya yaitu dengan memisalkan: x⁴+5 = U serta = 4x³, sehingga x³ dx = 1/4 dU  .

Berdasarkan pemisalan di atas, sehingga persamaan intergralnya yaitu:

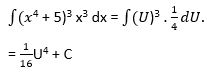
Apabila hasil diatas kemudian disubstitusikan dengan permisalan U maka akan diperoleh:

Contoh di atas adalah tehnik substitusi untuk integral tak tentu. Pada suatu kasus integral tertentu, dimana pada nilai interval a≤ b ≤c tertentu, sehingga intervalnya harus disubstitusi dalam interval baru bagi variabel U. contohnya f₀² (x⁴ + 5)³ x³ dx, dengan pemisalan:

X⁴ + 5= U dan , sehingga x³ dx=   Agar persamaan integral dalam U bisa tercipta, maka interval 0≤ x ≤2 diubah menjadi:

• X=0 → U= x⁴+5 = 0⁴= 5= 5
• X=2 → U= x⁴+5 =2⁴+5 =21

Dari permisalan di atas, maka persamaan integralnya yaitu:

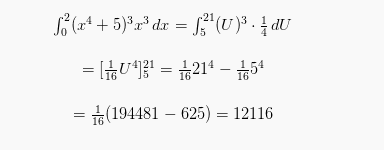
2. Integral Substitusi pada Fungsi Trigonometri

Pada beberapa kasus, trigonometri sebagai integran tidak dapat langsung diintegralkan layaknya rumus integral awal, sehingga diperlukan perubahan integral. Perubahan fungsi trigonometri bisa dilakukan seperti persamaan berikut ini:

• sin² A + cos² A = 1
• tan² A + 1 = sec² A
• cot² A + 1 = csc² A
• sin A cos A = ½ sin 2A
• sin² A = ½ – ½ cos 2A
• cos² A = ½ + ½ cos 2A
• sin A cos B = ½ [sin (A + B) + sin (A – B)]
• cos A sin B = ½ [sin (A + B) – sin (A – B)]
• cos A cos B = ½ [cos (A + B) + cos (A – B)]
• sin A sin B = – ½ [cos (A + B) – cos (A – B)]

Seperti halnya fungsi aljabar, fungsi trigonometri bisa menggunakan rumus substitusi jika integran terdiri atas perkalian fungsi dengan fungsi turunan. Cara pengoperasiannya juga sama dengan fungsi aljabar. Contohnya jika 2x sin(x² + 1)dx, untuk memperoleh integralnya yaitu dengan pemisalan:

X2 + 1= U serta , maka 2x dx= dU

Atas permisalan tersebut, sehingga persamaan integralnya jadi:

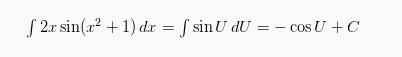
Apabila hasil integral tersebut disubstitusikan dengan permisalan U, maka akan diperoleh:

-cos U + C = -cos(x²+1) + C

Atau apabila fungsi turunannya merupakan fungsi trigonometri langsung, maka contohnya  akan memperoleh integralnya dengan memisalkan:

Cos x = U serta  sehingga sin x dx= -dU.

Dari pemisalan tersebut, sehingga persamaan integralnya yaitu:

3. Substitusi dengan Integran

Dengan teknik ini, bisa dimisalkan dengan yⁿ = ax + b penyelesaian integral pada fungsi f(y) memakai teknik substitusi seperti pertama. Contohnya  dimisalkan menjadi: y² = x + 3y² ataupun y² – 3 = x  sehingga diperoleh  ataupun 2y dx = dy.

Dari permisalan di atas, makan akan diperoleh persamaan integral yaitu:

4. Substitusi dengan Integran

Integral berintegran akar seperti yang tadi telah disinggung, bisa kamu kerjakan dengan pemisalan bentuk akar tersebut, yaitu:

B. Integral Parsial

Setelah integral substitusi, kini kita akan membahas integral parsial. Dimana integral parsial digunakan di saat teknik substitusi tidak bisa diterapkan. Adapun konsep dari integral parsial yaitu:

Jika y= U(x).V(x), sehingga U’.(x) + U(x).V’. (x)

Apabila y digantikan UV sehingga

d(UV) = V(x).U’(x)dx + U(x).V’(x)dx

Sebab, diketahui bahwa V’(x)dx = dV serta U’(x)dx = dU sehingga diperoleh persamaan:

d(UV) = v.dU + U.dV

U.dV = d(UV) – V.dU

Dengan kedua ruas persamaan tersebut diintegralkan, maka diperoleh rumus integral parsial:

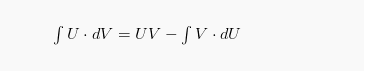
Dalam menerapkan substitusi parsial, ada beberapa hal yang harus diperhatikan, yaitu pemilihan U serta dV yang tepat supaya pengintegralan membuahkan hasil. (dV) harus yang bisa diintegralkan dengan rumus, kemudian yang lain jadi U.

Dalam integral parsial tidak jarang bisa menurunkan U serta mengintegralkan  dV secara berulang, namun proses bisa diringkas lho. Contohnya pada  yaitu:

Sehingga diperoleh hasil:

= (x² . Sin x) – (2x . cos x) + (2.-sin x) + C

= x² sin x + 2x cos – 2 sin + C

Ya, kita telah selesai membahas mengenai integral substitusi dan integral parsial, selanjutnya yaitu contoh soal dan pembahasan seputar materi di atas. Yuk simak aja ya!

Contoh Soal Integral Substitusi dan Integral Parsial serta Pembahasannya

1. Contoh soal integral substitusi.

Tentukan hasil dari soal integral di bawah ini:

 2x sin 2x dx

Penyelesaian:

Misalnya U = cos 2x serta  = -2 sin 2x, sehingga dU= -2 sin 2x dx

–  sin 2x dx

Sehingga:

disubstitusikan menggunakan nilai U menjadi :

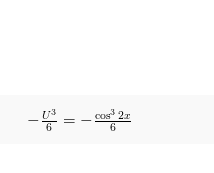
Contoh soal kedua:

Tentukan hasil dari soal di bawah ini!

Penyelesaian:

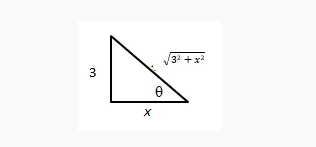
Nilai x = 3 tan  serta dx= 3sec²  d  serta x²= 9 sec²

Sehingga :

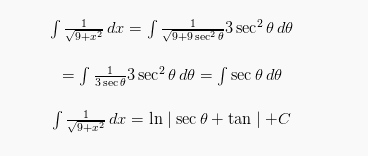
Menggunakan segitiga di atas, maka nilai sec serta tan dapat diketahui. Sehingga:

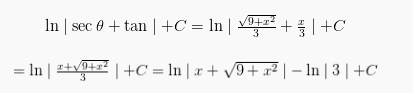
Nah, itu dia soal serta pembahasan mengenai integral substitusi dan integral parsial yang dapat kami sampaikan. Mempelajari suatu materi tentu saja lebih mudah melalui soal serta pembahasannya bukan? Jika kamu belum begitu paham dan mengerti, mengulangi materi terkait adalah satu langkah yang tepat untuk lebih menguasainya. Semangat dan selamat berlajar ya!