Geometri Bidang Datar – Dari sekian banyak ilmu dasar pada matematika, ada satu lagi yang mesti kamu kuasai, yakni transformasi geometri dan geometri bidang datar. Pasalnya, ilmu ini akan berguna banget untuk mendukung berbagai ilmu lain, mulai dari Kimia, Fisika, dan masih banyak lagi. Pada materi ini, beberapa yang akan kamu pelajari adalah jenis bangun datar, sifatnya, serta penghitungan keliling dan luasnya.
Materi geometri bidang datar ini adalah salah satu yang paling banyak dikembangkan peradaban masa lalu. Rumus-rumusnya banyak digunakan untuk mengukur luas daerah maupun luas benda. Mengetahui materi ini akan sangat bermanfaat saat kamu akan mempelajari geometri bangun ruang nantinya.
Mengenal Geometri Bangun Datar
Dari ulasan di atas, tentunya kamu sudah tahu gambaran mengenai materi ini. Namun, biar lebih afdhol, kamu juga harus mengerti definisinya, biar tidak salah persepsi, ya! Nah, geometri sendiri merupakan ilmu yang mempelajari tentang hubungan di antara objek geometri. Mulai dari titik, garis, bangun, serta sudut.
Geometri adalah cabang Matematika yang paling tua dalam sejarah. Ilmu ini juga dipelajari oleh beberapa ilmuwan seperti Pythagoras, Thales, Euclid, dan sebagainya. Pada geometri, akan dibahas juga tentang konsep jarak yang meliputi jarak dua titik ataupun jarak dari titik ke garis. Pun, akan dibahas mengenai titik tengah dari dua titik.
Nah, kamu kan sudah tahu kalau ada empat objek pembahasan pada geometri. Kali ini, yang akan kita dalami adalah geometri bangun datar. Bangun sendiri merupakan beberapa garis yang saling berhubungan serta memenuhi syarat tertentu.
Jadi, bisa disimpulkan bahwa pengertian geometri bangun datar adalah suatu bentuk geometris yang terdiri atas dua dimensi ataupun hanya mempunyai luas, tapi tidak mempunyai volume. Beberapa jenis bidang datar adalah lingkaran, segiempat, segitiga, dan sebagainya.
Kedudukan Titik dan Garis Pada Bidang
Setelah mengetahui pengertian dari geometri bangun datar, kamu harus tahu kedudukan titik serta garis di suatu bidang. Materi ini harus banget kamu tahu agar bisa mengerjakan soal-soal nantinya. Langsung saja, ini dia ulasannya!
Kedudukan Titik pada Garis
Semisal, ada garis AB serta dua titik yakni X dan Y, sehingga bisa digambarkan sebagai berikut:

Dari gambar tersebut, bisa diketahui bahwa titik ada pada garis AB, sedangkan titik Y ada di luar garis AB.
Kedudukan Titik pada Bidang
Coba kamu lihat gambar di bawah ini!
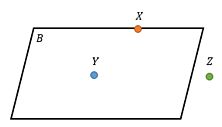
Pada bidang datar B ini, ada tiga titik, yakni X, Y, dan Z. Sehingga, bisa disimpulkan bahwa titik x tepat ada di bidang B, Y ada di dalam bidang B, sedangkan titik Z ada di luar bidang B.
Kedudukan Garis pada Bidang
Nah, untuk kedudukan garis pada bidang, terbagi menjadi empat yakni saling sejajar, saling berpotongan, saling berimpit, dan saling bersilangan. Dua garis akan disebut saling sejajar jika dua garis itu ada pada bidang yang sama, tidak mempunyai titik perpotongan, serta jarak antara garis selalu tetap.
Sedangkan dua garis dikatakan saling berpotongan jika ada pada bidang sama serta saling bertemu pada salah satu titik (titik persekutuan). Dua garis disebut berimpit jika sama-sama terletak di satu garis lurus di bidang yang sama. Terakhir, dua garis saling bersilangan jika tidak ada pada bidang yang sama, tidak berpotongan, serta tidak saling sejajar.
Selain itu, kamu juga harus mengenal hubungan antar sudut. Yuk, simak di bawah ini!
Hubungan Antar Sudut
Hubungan antar sudut terbagi menjadi empat, yakni sudut saling berpenyiku, berpelurus, bertolak belakang, dan dua garis sejajar yang dipotong oleh garis yang lain.
Sudut berpenyiku akan terbentuk jika salah satu sudutnya adalah penyiku dari sudut lainnya. Contohnya seperti pada gambar di bawah ini!
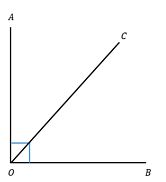
Jadi, < BOC adalah penyiku dari <AOC. Yang dimaksud berpenyiku adalah <BOC + <AOC = 90o
Sudut berpelurus adalah dua sudut yang membentuk sudut lurus atau 180o. Bisa kamu lihat pada gambar ini!
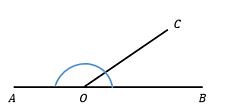
Dimana <BOC adalah pelurus <AOC dan sebaliknya. Jadi, hubungan saling berpelurus bisa terjadi jika <BOC + < AOC = 180o.
Selanjutnya, ada sudut saling bertolak belakang dimana dua sudut mempunyai arah hadap saling berlawanan. Sudut-sudut saling bertolak belakang akan mempunyai besar sudut sama.
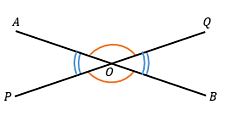
<BOQ = <POA, serta <POB = <AOQ.
Terakhir, ada hubungan antar sudut berupa dua garis sejajar dipotong dengan garis yang lain. Nah, untuk yang satu ini, ada pembahasan khusus, sebab, ada beberapa keadaan yang harus kamu tahu.
Coba kamu lihat gambar berikut ini:
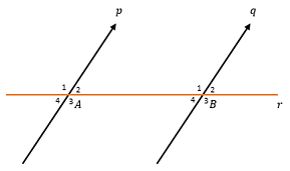
- Sudut sehadap adalah sudut yang menghadap pada arah yang sama, seperti <A1 dan <B1, <A4 dan <B4, <A2 dan <B2, dan juga <A3 dan <B3.
- Sudut dalam berseberangan yakni sudut yang letaknya ada di dalam garis p dan q dengan keadaan letak yang berseberangan. Seperti pada <A2 dan <B4 dan juga <A3 dan <B1.
- Sudut luar berseberangan yakni yang letaknya ada di luar dari garis p dan q serta letaknya saling berseberangan seperti <A1 dan <B3, lalu, ada lagi yakni <A4 dan <B2.
- Sudut dalam sepihak adalah sudut yang ada di garis p dan q serta memiliki letak pada sisi yang sama seperti pada <A2 dan <B1, serta <A5 dan <B4.
- Sudut luar sepihak adalah yang letaknya ada di luar garis p dan q serta memiliki letak pada sisi yang sama seperti pada <A1 dan <B2, serta <A dan <B3.
Keliling dan Luas Bangun Datar
Setelah mengenal dasar-dasar geometri bidang datar, kamu bisa menyimak juga materi tentang keliling dan luasnya. Yuk, cari tahu rumusnya di bawah ini!
Bujur Sangkar
Bujur sangkar bisa disebut dengan persegi. Dimana merupakan bangunan segi emat dengan empat sisi yang sama panjang. Keempat sudut bujur sangkar berbentuk siku-siku.
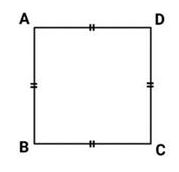
Rumus keliling : K = 4s
Rumus Luas : L = s x s atau L = s2
Persegi Panjang
Persegi panjang adalah bangunan segi empat yang dua sisi saling berhadapan memiliki panjang yang sama. Keempat sudutnya merupakan sudut siku-siku.
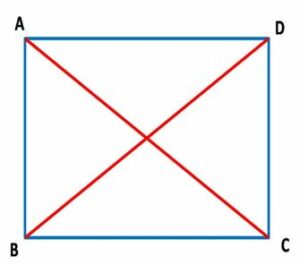
Rumus Keliling : K = 2p + 2l
Rumus Luas : L = p x l
Segitiga
Adalah bangun datar dengan jumlah sudut sebesar 180o dan dibentuk dengan menghubungkan tiga titik yang tidak segaris pada suatu bidang. Ada empat jenis segitiga, yakni segitiga sama kaki, segitiga sama sisi, segitiga siku-siku, dan segitiga sembarang.
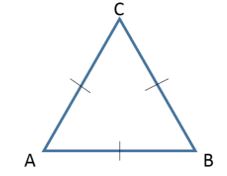
Rumus Keliling : K = 3s
Rumus Luas : L = ½ x alas x tinggi
Jajar Genjang
Jajar genjang adalah bangun dengan dua pasang sisi saling sejajar.
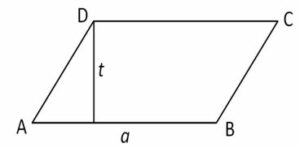
Rumus Keliling : K = 2 (p + l)
Rumus Luas : L = alas x tinggi
Layang-Layang
Layang-layang adalah bangun dengan dua pasang sisi sama panjang.
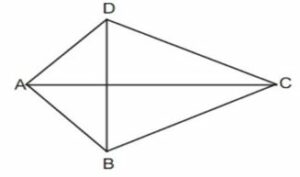
Rumus Keliling : AB + BC + CD + DA
Rumus Luas : ½ . d1 . d2
Diagonal 1 atau d1 = 2 x L / d2
Diagonal 2 atau d2 = 2 x L / d1
Demikian pembahasan tentang geometri bangun datar yang bisa kamu pelajari. Pastikan kamu juga mencari soal-soalnya agar pengetahuanmu semakin sempurna, ya!