Relasi dan Fungsi: Pengertian, Contoh Soal dan Pembahasannya

Relasi dan Fungsi – Untuk beberapa siswa, pelajaran matematika sering kali dianggap suatu pelajaran yang menakutkan. Padahal sebenarnya jika kita menyukai mata pelajaran tersebut, semuanya akan terasa begitu menyenangkan dan menjadi mudah dimengerti.

Relasi dan fungsi merupakan materi pembelajaran dasar untuk memasuki materi lain seperti turuanan, limit fungsi maupun yang lainnya. Sehingga kamu harus benar-benar mengerti dan memperhatikan ulasan yang akan dijelaskan berikut ini. Jangan ngelamun ya hehe.

Adapun materi yang akan kita bahas pada kesempatan kali ini yakni tentang relasi dan fungsi, yang mana kita akan bahas mulai dari pengertian relasi dan fungsi, contoh soal relasi dan fungsi beserta cara penyelesaiannya sampai ketemu dengan jawabannya.

Relasi

Contoh relasi:

A = {0,1,2,5}

B = {1,2,3,4,6}

Selanjutnya hasil dari relasi keduanya dapat disajikan ke dalam beberapa bentuk, yaitu diagram cartesius, diagram panah dan himpunan pasangan berurutan, serta rumus yaitu seperti di bawah ini:

1. Diagram Panah

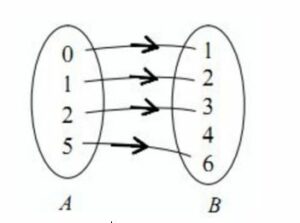
Bentuk pertama yang bisa kita buat dari relasi himpunan A dan himpunan B di atas adalah diagram panah. Agar kamu lebih bisa memahami, perhatikan gambar contoh diagram panah di bawah ini.

Coba perhatikan diagram panah tersebut, maka bisa kita lihat, 0 merupakan relasi dari 1, 1 merupakan relasi dari 2, dan seterusnya.

1. Diagram Cartecius

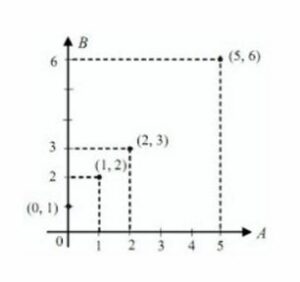
1. Himpunan Pasangan Berurutan

R= {(0,1) , (1,2) , (2,3) , (5,6)}

R merupakan hasil relasi dari domain dengan kodomain.

1. Rumus

f(x)= x+1, dimana x € {0,1,2,5} dan f(x) € {1,2,3,4,6}

Mengapa demikian? Karena jika setiap anggota himpunan A ditambahkan 1 (+1) maka akan  menjadi anggota himpunan B . Seperti 0+1=1 ; 1+1=2 dan seterusnya.

Fungsi

Jika sebelumnya dalam bab relasi kita menyebutnya relasi dari himpunan A dan himpunan B. Maka lain ceritanya dalam materi fungsi, kita akan menyebutkan fungsi dari A ke B dimana setiap anggota dari himpunan A berpasangan dengan satu anggota himpunan B yang tepat.

Sama dengan relasi, fungsi atau pemetaan juga dapat disajikan/ dinyatan dalam diagram panah, diagram cartecius, rumus dan himpunan pasangan berurutan. Fungsi f dari himpunan A ke himpunan B dinyatakan dalam notasi:

f: A → B

Dengan penjelasan:

• A merupakan daerah asal atau domain dilambangkan (dinotasikan) D
• B merupakan daerah kawan atau kodomain dinotasikan K
• Dan daerah hasil disebut dengan range dinotasikan R

Biasanya, materi seperti ini akan lebih mudah dipahami jika sudah mengetahui langsung contoh soalnya kan? Nah yuk cek cek contoh soalnya berikut ini.

Contoh soal fungsi:

A = {1,2,3,4} dan B = {1,2,3,4,5,6,7,8}

Suatu fungsi f : A   → B ditentukan oleh f(x)= 2x-1.

Persoalan :

1. Tentukan himpunan C (range) dari fungsi f di atas!
2. Sajikan fungsi f dengan diagram panah!
3. Sajikan fungsi f ke dalam grafik (diagram cartecius) !

Penyelesaian :

1. f(x)= 2x-1. Maka

f(1)= 2.1 -1 = 1

f(2)= 2.2 -1 = 3

f(3)= 2.3 -1 = 5

f(4)= 2.4 -1 = 7

jadi, range atau hasil dari fungsi f yaitu {1,3,5,7}

1. Maka diagram panah dari fungsi f di atas sebagai berikut:

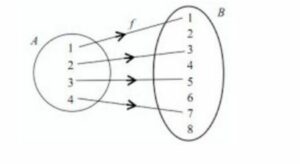
1. Grafik fungsi dari himpunan A ke B di atas yaitu:

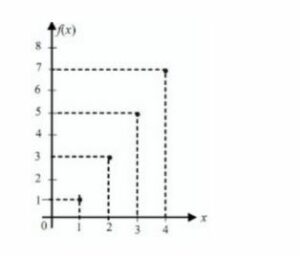
Macam-Macam Fungsi

Adapun macam-macam fungsi di dapat dibagi menjadi 7 yaitu fungsi konstan atau fungsi tetap, fungsi linier, fungsi kuadrat, fungsi identitas, fungsi tangga, fungsi mutlak atau fungsi modulus, fungsi ganjil atau fungsi genap. Adapun pembahasannya mulai dari pengertian, contoh soal dan cara penyelesaiannya dapat kamu simak dibawah ini.

1. Fungsi Konstan atau Fungsi Tetap

Pengertian fungsi konstan adalah sebuah fungsi dimana f: A→B yang ditentukan rumus f(x), disebut fungsi konstan jika setiap anggota asal selalu f(x)=C. Dengan syarat C adalah bilangan konstan. Agar lebih jelas, yuk kita perhatikan contoh berikut ini.

Contoh soal fungsi konstan

Diketahui :

f: R→R dengan rumus f(x)=3

Daerah domain {x|-3≤ x <2} . Maka nyatakan dalam diagram grafik dari fungsi tersebut!

Penyelesaian:

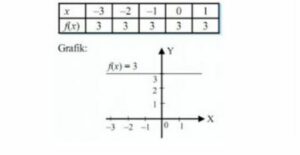
2. Fungsi Linier

Pengertian fungsi linier adalah fungsi f(x)= ax+b, dimana a ≠0, a dan b termasuk bilangan konstan atau tetap. Untuk grafiknya berbentuk garis lurus, ini sangat berbeda dengan grafik konstan yang pada umumnya berbentuk garis horisontal. Untuk lebih jelasnya, silahkan cermati contoh soal berikut ini.

Contoh soal fungsi linier:

Diketahui f(x)= 2x + 3, coba nyatakan dalam diagram garfik.

Penyelesaian :

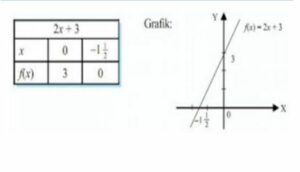
3. Fungsi Kuadrat

Merupakan sebuah fungsi dengan f(x)= ax²+bx+c, dimana a≠0 serta a, b dan c adalah bilangan konstan. Fungsi kuadrat memiliki bentuk diagram grafik menyerupai parabola, agar lebih mudah dipahami, pehatikan contoh soal berikut ya.

Contoh soal :

Diketahui fungsi f(x)= x²+2x-3, perhatikan diagram berikut!

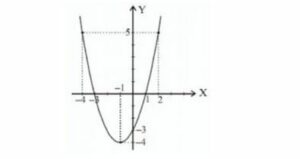
Tentukan:

1. Domain dari fungsi f
2. Niai minimum dari fungsi f
3. Nilai maksimum dari fungsi f
4. Range fungsi f
5. Koodinat titik balik minimum

Penyelesaian:

1. Domain dari fungsi f di atas yaitu {x|-4≤ x <2}
2. Nilai minimum dari fungsi f di atas yaitu -4
3. Nilai maksimum dari fungsi f di atas yaitu 5
4. Range dari fungsi f yaitu {y|-4≤ x <5}
5. Koordinat titik balik minimum dari grafik fungsi f di atas yaitu (-1, -4)

4. Fungsi Identitas

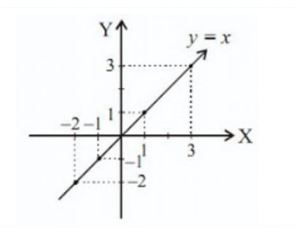
Pengertian fungsi identitas adalah fungsi dimana f(x)=x . Diagram grafik dari fungsi identitas berupa garis lurus.

Contohnya:

f(-2)= -2

f(0)= 0

f(1)= 1

f(3)= 3

maka gambar grafiknya:

5. Fungsi Tangga

Pengertian fungsi tangga adalah fungsi f(x) yang mana berbentuk interval sejajar.

Perhatikan contoh soal fungsi tangga di bawah ini:

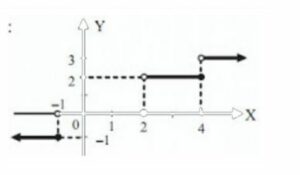
Diketahui f(x) = -1, jika x<1=0, jika -1< x <2 =2, jika 2< x <4=3, jika x> 4. Maka tentukan interval yang terbentuk dari:

a. f(-2)

b. f(0)

c. f(3)

d. f(3)

e. grafik dari interval yang terbentuk

jawab:

a. f(-2)= -1

b. f(0)= 0

c. f(3)= 2

d. f(3)= 3

e.

6. Fungsi Mutlak atau Modulus

Yaitu fungsi yang memasangkan setiap bilangan real dengan domain fungsi menjadi nilai mutlak. Misalkan:

7. Fungsi Ganjil atau Fungsi Genap

Pengertian fungsi ganjil atau fungsi genap adalah Sebuah fungsi f(x) akan disebut sebagai fungsi ganjil jika f(-x)= -f(x) dan disebut fungsi genap jika f(-x)= f(x).

Kemudian fungsi f(-x) ≠-f(x) serta f(-x) ≠f(x) maka bukan termasuk dari kedua fungsi tersebut. Coba perhatikan contoh soal fungsi ganjil atau fungsi genap berikut ini:

Tentukan fungsi di bawah ini apakah fungsi ganjil atau fungsi genap atau tidak.

1. f(x)= 2x³+x
2. f(x)= x² – 8x

penyelesaian:

1. f(x) = 2x³+x

f(-x) = 2(-x) ³+(-x)

= -2x³ -x

= -(2x³+x)

= -f(x)

Jadi, fungsi tersebut merupakan fugsi ganjil.

1. f(x)= x²-8x

f(-x)= (-x) ² -8(-x)

= x²+ 8x

fungsi f(-x) ≠ -f(x) dan f(-x) ≠f(x)

jadi, fungsi diatas bukan merupakan fungsi genap maupun fungsi ganjil.

Nah, itu dia ulasan mengenai relasi dan fungsi lengkap dengan contoh soal beserta cara penyelesaiannya hingga ketemu jawabannya hehe. Cermati baik-baik dan perhatikan contoh soal yang ada ya. Cintai dulu matematika maka matematika akan mencintai kamu. Semangat belajarnya ya!