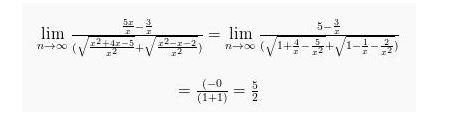Materi limit fungsi – Pasti kamu pernah mendengar kata limit, limited bukan? kata limit yang biasa kita dengar berarti sedikit atau mendekati, misalnya limited edition ini berarti persediaan yang sedikit atau mendekati habis. Hal tersebut sama halnya dengan limit fungsi aljabar.
Pengertian Limit Fungsi
Limit dalam hal ini berarti menuju batas, mendekati, hampir, dekat tapi tak bisa tercapai, hanya mengagumi dari jauh, baper hehe. Nah, agar kamu lebih mudah memahami dan mengerti mengenai limit fungsi aljabar, perhatikan materi limit fungsi di bawah ini ya:
Limit Fungsi Aljabar
Seperti yang telah disinggung sebelumnya, pengertian limit fungsi aljabar adalah mendekati, mengapa meski ada limit tidak dicapai saja? Ya, karena limit tersebut menjelaskan mengenai suatu fungsi ketika batas tertentu didekati. Mengapa meski didekati? Karena, pada dasarnya suatu fungsi tidak terdefinisi berada pada titik tertentu.
Walaupun suatu fungsi tidak terdefinisi, namun nilai yang didekati oleh fungsi tersebut masih dapat dicari apabila tiitk tertentu didekati oleh limit yang sebelumnya telah dijelaskan di atas.
Rumus Limit Fungsi Aljabar
Dalam matematika, pada umumnya limit memiliki rumus yang dituliskan dalam bentuk sebagai berikut:
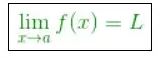
Dari rumus di atas, diketahui bahwa bila x mendekai a dimana x ≠a, maka f(x)berarti mendekati L. Pendekatan dari x ke a bisa dilihat dari 2 sisi, yaitu kanan dan kiri, atau bisa juga disebut dengan istilah limit kiri serta limit kanan.
Metode Limit Aljabar
Metode pendekatan dari x ke a atau pencarian limit memiliki 4 macam metode, kira-kira apa saja? Pendekatan chat WA, DM Instagram? Hehe bukan ya. Nah agar kamu lebih mudah memahaminya, simak ulasan lengkapnya di bawah ini ya.
1. Metode Subsitusi
Metode pencarian fungsi limit dengan subsutusi merupakan metode yang paling sederhana, yaitu hanya mengubah peubah yang paling mendekati dengan nilai pada fungsi aljabar tertentu.
Contoh:
= 3(2) – 1= 6-1 = 5
Maka nilai fungsi limit aljabar tersebut yaitu
= 5
2. Metode Pemfaktoran
Metode yang kedua yaitu pemfaktoran, metode ini digunakan apabila subsitusi fungsi limit menghasilkan nilai yang tak terdefinisikan.
Contoh:
Nah, masih saling berkaitan dengan metode kedua yaitu pemfaktoran, ada juga metode dalam menentukan limit fungsi dengan cara membagi penyebut dengan pangkat tertinggi serta mengalikannya dengan faktor sekawan. Perhatikan materinya pada poin berikut ini ya.
3. Membagi dengan Pangkat Tertinggi Penyebut
Dari namanya sudah ada gambaran kan? Jadi, metode yang ketiga ini kamu bisa mencari limit fungsi dengan cara membagi dengan pangkat tertinggi dari penyebut. Jangan Cuma dibayangin, yuk praktekin dengan memperhatikan penerapannya di bawah ini ya.
Selain contoh di atas, ada juga nih contoh berikutnya, yaitu:
Tentukan nilai limit aljabar pada fungsi limit di bawah ini!
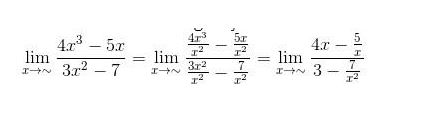
Besarnya pangat tertinggi penyebut pada limit di atas adalah 3, sehingga akan diperoleh,
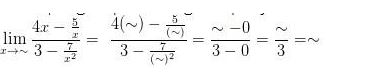
Jadi, besarnya nilai limit fungsi aljabar pada soal di atas adalah
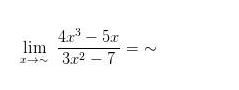
4. Metode Mengalikan dengan Faktor Sekawan
Metode terakhir yang bisa kamu gunakan dalam mencari nilai limit fungsi aljabar yaitu mengalikannya dengan faktor sekawan. Metoode tersebut bisa Anda gunakan jika metode subsitusi langung mengahasilkan nilai yang irasional.
Dalam metode ini, fungsi dikalikan dengan faktor sekawannya agar bentuk limit menjadi tidak irasional, sehingga selanjutnya dapat kembali disubsitusikan langsung dengan nilai x → c.
Contoh :
Tentukan nilai limit fungsi aljabar dari soal berikut ini!
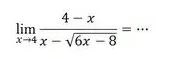
Langkah awal yang dilakukan guna mencari nilai limit fungsi aljabar yaitu menggunakan metode subsitusi dari x=c ke f(x), menjadi
Nah, bisa kamu lihat dari penyelesaian masalah di atas, ternyata nilai limit dari soal tersebut tak terdefinisi atau bentuk tak tentu yaitu , sehingga dalam menentukan nilai limit kamu harus menggunakan metode lain. Coba kamu perhatikan lagi, pada f(x) ternyata terdapat bentuk akar 
, dengan begitu kamu bisa menggunakan metode perkalian akar sekawan, sehingga menjadi :
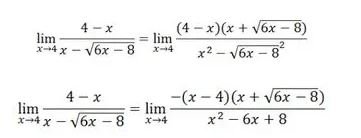
Bentuk x2-6x+8 kemudian difaktorkan menjadi:
Jadi, nilai limit fungsi aljabar dari persoalan di atas adalah -4
Teorema atau Pernyataan
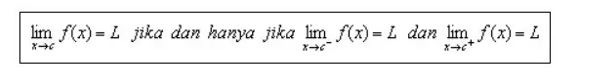
Sebuah fungsi bisa dikatakan memiliki limit apabila antara limit kanan serta limit kiri mempunyai besar nilai sama dan bila nilai limit kanan kirinyanya tidak sama, maka fungsi tersebut tidak memiliki nilai limit.Sifat Limit Fungsi Aljabar.
Jika n adalah bilangan bulat positif, f serta g fungsi yang mempunyai limit c dan k sebagai konstanta, sehingga berlaku sifat-sifat seperti di bawah ini:
Limit Fungsi Aljabar Tak Hingga
Dalam proses pengoprasian suatu limit fungsi aljabar, tidak menutup kemungkinan terdapat nilai x yang tak berhingga (∞). Oleh sebab itu, jika disubsitusikan akan menghasilkan nilai yang tidak menentu. Tidak hanya sampai disitu, apabila suatu fungsi memenuhi syarat dimana n adalah bilangan bulat, f serta g memiliki nilai limit terhadap c dan k adalah konstanta, maka akan berlaku sifat-sifat limit fungsi aljabar yang telah dijelaskan pada poin di atas.
Guna menyelesaikan soal limit fungsi aljabar dengan bentuk tak hingga dapat dilakukan dengan dua metode, yaitu:
1. Membaginya dengan Pangkat Tertinggi
Metode yang pertama yaitu dengan membagi menggunakan pangkat tertinggi, cara bisa diterapkan untuk limit fungsi dalam bentuk .
Metode ini bisa dilakukan dengan membagi pembilang f(x) serta penyebut ialah g(x) dengan variabel xn yang berpangkat tertinggi di dalam fungsi f(x) serta g(x). Dan selanjutnya, baru kamu mensubsitusikannya dengan x  → ∞.
Contoh :
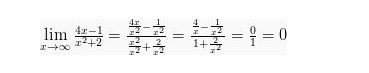
2. Mengalikan dengan Bentuk Sekawan
Metode mengalikan denga bentuk sekawan bisa diterapkan pada fungsu berbentuk 
. Cara yang satu ini dapat dituntaskan menggunakan perkalian bentuk sekawan, yakni:
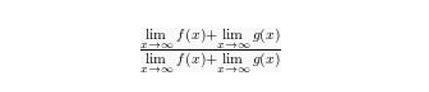
Selanjutnya, kamu bisa menggunakan motedo pertama yaitu membagi dengan pangkat yang tertinggi. Contohnya yaitu:
Langkah berikutnya pembilang serta penyebut dibagi dengan x pangkat tertinggi, menjadi :
Limit Fungsi Trigonometri
Apakah kamu tahu, bahwa limit juga bisa diterapkan dalam fungsi trigonometri lho. Secara umum, penyelesaiannya sama seperti fungsi limit aljabar, hanya saja kamu harus mengerti konsep trigonometri terlebih dahulu.
Penyelesaiian limit pada fungsi trigonometri dapat dilakukan dengan merubah bentuk tangen, cosinus maupun sinus. Dalam konsep ini terdapat 3 bentuk limit fungsi trigonometri, yaitu:
- Bentuk limx -> c f (x)
Merupakan nilai hasil dari subsitusi c ke x dari trigonometri.
Contohnya:
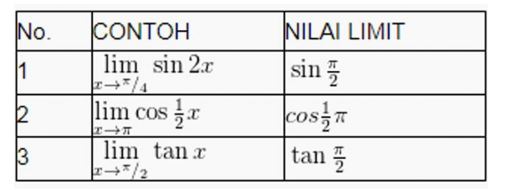
Namun, jika c=0 maka:
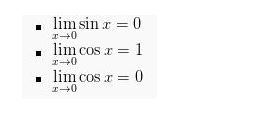
- Bentuk
Dalam bentuk yang kedua ini, terdapat 2 perbandingan dari trigonometri berbeda. Keduanya akan menghasilkan g©= 0 dan f©=0 jika disubsitusikan dengan c. sehingga limit trigonometrinya akan .
Contoh: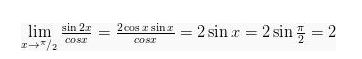 
- Bentuk
Bentuk yang ketiga, limit akan dihasilkan melalui perbandingan trigonometri dengan fungsi aljabar. Bentuk rumus dasar dari limit ini yaitu:
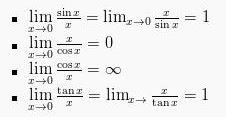
Kemudian dari rumus dasar di atas dapat dikembangkan menjadi:
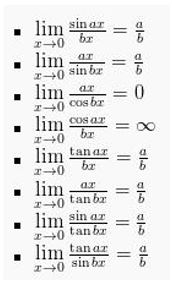
Nah, jadi itu dia segombyok materi seputar limit fungsi aljabar. Semuanya tidak serumit kelihatannya kok, kuncinya cintai dulu angka dan rumusnya yaa. Semangat !
