Pengertian persamaan kuadrat adalah suatu persamaan dari variabel-variabel yang memiliki pangkat paling tinggi dua. Bentuk umum dari persamaan kuadrat ialah:
ax2 + bx + c = 0
Dari persamaan di atas, diketahui a dan b adalah koefisien dan c merupakan konstanta, serta a tidak sama dengan 0 atau termasuk pertidaksamaan dari 0.
Proses untuk memecahkan atau menyelesaikan persoalan dari sebuah persamaan sendiri biasanya disebut akar-akar persamaan kuadrat. Akar-akar adalah nilai dari variabel x atau y yang sesuai persamaan tersebut. Dengan kata lain, nilai tersebut bisa disubstitusikan dalam persamaan tersebut dan menghasilkan nilai nol.
Akar-Akar Persamaan Kuadrat
Dalam ilmu matematika, ada tiga metode yang bisa diterapkan untuk mencari akar PK ax2 + bx + c = 0, yakni metode pemfaktoran, kuadrat sempurna, dan rumus abc. Oke langsung saja simak pembahasan dari 3 metode ini, untuk mencari akar persamaan kuadrat dibawah ini.
1. Pemfaktoran
Dibanding dua faktor lain, pemfaktoran adalah metode yang paling mudah digunakan jika bilangannya rasional. Di bawah ini adalah tabel model persamaan kuadrat dan penerapan metode pemfaktoran.
| No | Persamaan Kuadrat | Faktorisasi Akar-akar |
| 1 | x2 + 2xy + y2 = 0 | (x + y)2 = 0 |
| 2 | x2 – 2xy + y2 = 0 | (x – y)2 = 0 |
| 3 | x2 – y2 = 0 | (x + y)(x – y) = 0 |
Jika Anda ingin menggunakan metode ini, pertama-tama Anda harus mengetahui model PK yang hendak diselesaikan. Setelah model persamaan kuadratnya diketahui, selanjutnya pemfaktoran bisa diaplikasikan sesuai dengan bentuk yang tertera pada tabel di atas.
Untuk lebih jelasnya, berikut adalah contoh penyelesaian PK 5x2+13x+6=0 dengan metode pemfaktoran.
Jawab:
5x2 + 13x = 6 = 0
5x2 + 10x + 3x + 6 = 0
5x(x + 2) + 3(x + 2) = 0
(5x + 3)(x + 2) = 0
5x = -3
x = -3/5, atau x = -2
Sehingga, himpunan penyelesaian HP = (-3/5, -2)
2. Kuadrat Sempurna
Meski mudah, sayangnya tidak semua PK bisa dicari dengan metode pemfaktoran atau faktorisasi. Jika demikian, Anda bisa menggantinya dengan metode kuadrat sempurna. Caranya yakni dengan melengkapkan kuadrat sempurna. Bentuk PK sempurna ialah bentuk persamaan yang mana hasilnya adalah bilangan rasional.
Penyelesaikan PK dengan metode kuadrat sempurna bisa Anda lakukan dengan menerapkan rumus:
(x+p)2 = x2 + 2px + p2
Selanjutnya, ubah dalam bentuk persamaan (x+p)2 = q
Agar lebih jelas, silahkan simak contoh penyelesaian PK dengan metode kuadrat sempurna dari persamaan x2 + 6x + 5 = 0 berikut ini.
Jawab:
x2 + 6x +5 = 0
Ubah dalam bentuk x2 + 6x = -5
Kemudian tambahkan satu angka pada ruas kiri dan kanan sehingga berubah jadi kuadrat sempurna. Angka yang ditambahkan diambil dari separuh angka koefisien yang asalnya dari nilai x atau separuh 6, kemudian dikuadratkan jadi 32 = 9.
Kemudian tambahkan angka 9 pada ruas kiri dan kanan sehingga persamaannya menjadi:
x2 + 6x + 9 = -5 + 9
x2 + 6x + 9 = 4
(x+3)2 = 4
(x+3) = √4
x = 3 ± 2
- Untuk x+3 = 2
x = 2-3
x = -1
- Untuk x+3 = -2
x = -2-3
x = -5
Jadi, nilai akhirnya adalah, x= -1 atau x = -5
3. Rumus Kuadrat atau Rumus ABC
Metode lain yang bisa digunakan untuk menyelesaikan persamaan kuadrat adalah rumus abc. Rumus yang digunakan untuk metode ini adalah
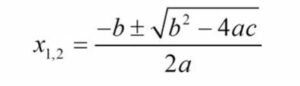
Berikut ini contoh penyelesaian persamaan kuadrat x2 + 4x – 12 = 0 dengan rumus abc.
Jawab:
x2 + 4x – 12 = 0
a=1, b=4, c=-12
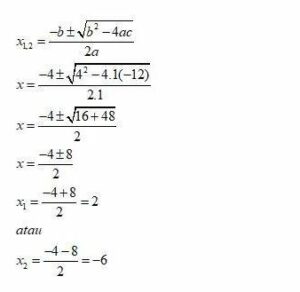
Jenis Akar-Akar Persamaan Kuadrat
Untuk mengetahui jenis akar-akar PR ax2 + bx + c = 0, Anda bisa mencari tahu nilai “Diskriminan” (D) yang terdapat pada rumus abc, yakni:
D = b2 – 4ac
Jadi rumus yang didapatkan adalah: x1,2 = -b + sqrtD/2a
Tanda akar D ini menentukan jenis akar-akar PD, apakah termasuk bilangan real atau bukan. Jadi akar-akar PK dari ax2 + bx + c = 0 ialah:
- Jika D > 0, berarti akar-akarnya real.
- Jika D < 0, berarti akar-akarnya tidak real.
- Jika D = 0, berarti akar-akarnya real dan kembar atau sama.
Penyusunan Persamaan Kuadrat Baru
Untuk menyusun persamaan kuadrat baru, Anda perlu mengetahui nilai akarnya terlebih dahulu. Hal ini bisa diketahui dengan mensubstitusikan nilai dari akar-akar yang sudah di ketahui pada persamaan:
(x – x1)(x – x2)
Meski begitu, PK baru juga bisa dibentuk meski nilai akar-akarnya tidak diketahui. Namun dengan syarat, jika akar-akarnya mempunyai relasi dengan akar-akar dari persamaan kuadrat lain.
Contoh Soal Persamaan Kuadrat dan Penyelesaiannya
Adapun beberapa contoh soal persamaan kuadrat dan penyelesaiannya dapat kamu pelajari seperti yang ada dibawah ini.
Contoh Soal Persamaan Kuadrat #1
Diketahui bentuk persamaan x2 – 4 = 3(x – 2) adalah ax2 + bx + c = 0. Tentukan nilai a, b, dan c secara berurutan.
A. 1, -2, 3
B. 1, -3, 2
C. 1, -3, -10
D. 1, 3, -2
Jawab:
Pertama, ubah persamaan di atas dalam bentuk umum terlebih dahulu:
⇒ x2 – 4 = 3(x – 2)
⇒ x2 – 4 = 3x – 6
⇒ x2 – 4 – 3x + 6 = 0
⇒ x2 – 3x + 2 = 0
⇒ a = 1, b = -3, dan c = 2
Maka jawaban yang benar adalah B.
Contoh Soal Persamaan Kuadrat #2
Diketahui salah satu akar pada persamaan kuadrat x2 + 2x + c = 0 adalah 3. Tentukan akar lainnya.
A. X = 3
B. X = 5
C. X = -5
D. X = -15
Jawab:
Pertama, substitusikan terlebih dahulu nilai x = 3 untuk mencari tahu nilai c.
⇒ x2 + 2x + c = 0
⇒ 32 + 2(3) + c = 0
⇒ 9 + 6 + c = 0
⇒ 15 + c = 0
⇒ c = -15
Selanjutnya substitusikan nilai c pada persamaan.
⇒ x2 + 2x + c = 0
⇒ x2 + 2x – 15 = 0
Berikutnya tentukan nilai akar dengan metode faktorisasi atau pemfaktoran:
⇒ (x + 5)(x – 3) = 0
⇒ x = -5 atau x = 3
Jadi jawaban yang benar adalah C.
Contoh Soal Persamaan Kuadrat #3
Jika akar-akar persamaan x2 – 3x – 10 = 0 adalah x1 dan x2, tentukan hasil x1 + x2.
A. x1+ x2 = 4
B. x1+ x2 = 3
C. x1+ x2 = 7
D. x1+ x2 = 5
Jawab:
Gunakan metode faktorisasi:
⇒ x2 – 3x – 10 = 0
⇒ (x + 2)(x – 5) = 0
⇒ x1 = -2 atau x2 = 5
Maka jumlah akar-akarnya adalah:
⇒ x1 + x2 = -2 + 5
⇒ x1 + x2 = 3
Selanjutnya gunakan metode cepat:
Dari: x2 – 3x – 10 = 0
Dik: a = 1, b = -3, c = -10
Ditemukan jumlah akarnya:
⇒ x1 + x2 = -b/a
⇒ x1 + x2 = -(-3)/1
⇒ x1 + x2 = 3
Jadi jawaban yang benar adalah B.
Bentuk soal yang sering keluar untuk materi persamaan kuadrat sendiri sangat beragam. Namun untuk ujian nasional, umumnya dalam bentuk soal cerita singkat.

