Idenfinite Integral/Antiderivatif atau yang lebih akrab disebut integral tak tentu adalah sebuah bentuk operasi integral dalam suatu fungsi, dan bisa menghasilkan fungsi baru.
Dalam konsep ini, fungsi utama belum memiliki nilai pasti, sehingga pengintegralan fungsi ini disebut dengan integral tak tentu. Selain diaplikasikan pada fungsi yang belum memiliki nilai pasti, integral juga bisa dioperasikan dalam fungsi trigonometri.
Sebelum lanjut membahas rumus dan contoh soalnya, kamu harus tahu secara jelas, pengertian integral tak tentu dan integral trigonometri.
Pengertian Integral
Integral adalah bentuk operasi matematika yang menjadikan invers/kebalikan dari sebuah limit pada suatu luas area tertentu.
Dari pengertian umumnya ini, integral bisa dikategorikan menjadi dua jenis, yakni integral sebagai invers dari turunan, yang disebut dengan integral tak tentu. Dan integral sebagai limit dari jumlah/luas suatu area yang kemudian disebut integral tentu.
Integral Tak Tentu
Seperti yang sudah disebutkan pada poin di atas, Jadi Pengertian integral tak tentu adalah invers atau kebalikan dari sebuah turunan. Turunan dari sebuah fungsi, apabila diintegralkan maka akan menghasilkan fungsi baru.
Coba deh kamu perhatikan turunan dari fungsi aljabar berikut:
- Turunan fungsi aljabar y = x3– 6 adalah yI = 3x2
- Turunan fungsi aljabar y = x3+ 17 adalah yI = 3x2
- Turunan fungsi aljabar y = x3+ 8 adalah yI = 3x2
- Turunan fungsi aljabar y = x3adalah yI = 3x2
Setelah mempelajari materi turunan, kamu akan tahu jika variabel pada suatu fungsi pengalami penurunan pangkat. Nah, dari contoh di atas, bisa diketahui jika terdapat banyak fungsi yang mempunyai hasil turunan sama persis yakni yl = 3x2.
Dimana fungsi variabel x3 atau fungsi pada varabel x3 yang kemudian dikurangi atau ditambah suatu bilangan (contohnya: +8, +17 ataupun -6) mempunyai turunan yang sama.
Apabila hasil turunan tersebut diintegralkan, seharusnya akan menjadi fungsi-fungsi awal seperti saat sebelum diturunkan. Hanya saja, beberapa kasus menunjukkan jika fungsi awal pada suatu turunan tidak diketahui, maka dari itu, hasil integral dari turunan ini bisa dituliskan dalam bentuk:
f(x) = y = x3 + C
Dari bentuk tersebut, nilai C bebas berapapun, yang mana notasi C disebut dengan konstanta integral. Integral tak tentu dari sebuah fungsi bisa dinotasikan sebagai:
![]()
Dari notasi di atas, bisa dibaca integral terhadap x” notasi disebut dengan integral. Kemudian, integral dari fungsi f(x) itu sendiri ialah penjumlahan f(x) dengan C, atau:
![]()
Karena antara turunan dan integral memiliki kaitan satu sama lain, maka rumus integral bisa didapatkan dari rumus penurunan. Jika bentuk turunan adalah sebagai berikut:
![]()
Maka akan didapatkan rumus integral aljabar sebagai berikut:
![]()
Dengan syarat jika ![]()
Untuk lebih mudah memahaminya, kamu bisa lihat contoh integral fungsi aljabar berikut ini:
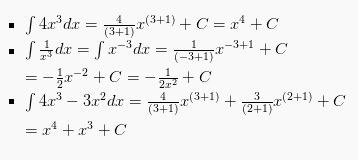
Integral Trigonometri
Pada penjelasan di atas sudah disebutkan, jika integral juga bisa dioperasikan dalam fungsi trigonometri. Konsep yang diterapkan pada integral trigonometri pun masih sama seperti integral aljabar. Yakni kebalikan dari sebuah penurunan, sehingga bisa disimpulkan jika:
| No. | Fungsi f(x) = y | Turunan | Integral |
| 1 | y = sin x | cos x | = sin x |
| 2 | y = cos x | – sin x | = – cos x |
| 3 | y = tan x | sec2 x | = tan x |
| 4 | y = cot x | – csc2 x | = – cot x |
| 5 | y = sec x | tan x . sec x | = sec x |
| 6 | y = csc x | -.cot x . csc x | = – csc x |
Selain menggunakan rumus di atas, kamu juga bisa menggunakan beberapa rumus berikut ini untuk pengoperasian integral trigonometri.
| Fungsi f(x) = y | Turunan | Integral |
| cos (ax + b) | = sin (ax + b) + C | |
| sin (ax + b) | = cos (ax + b) + C | |
| y = tan (ax + b) | sec2 (ax + b) | = tan (ax + b) + C |
| y = cot (ax + b) | csc2 (ax + b) | = cot (ax + b) |
| y = sec (ax + b) | tan (ax + b) . sec (ax + b) | (ax+b) . sec(ax + b) dx= sec (ax + b) + C |
| y = csc (ax + b) | cot (ax + b) . csc (ax + b) | cot (ax + b) . csc (ax + b) dx = csc (ax + b) |
Sifat Integral
Dari penjelasan di atas, kamu bisa menyimpulkan jika integral memiliki sifat-sifat, seperti:
- ∫ k . f(x)dx = k. ∫ f(x) (dengan k merupakan konstanta)
- ∫ f(x) + g(x)dx = ∫ (x)dx + ∫ g(x)dx
- ∫ f(x) – g(x)dx = ∫ f(x)dx – ∫ g(x)dx
Contoh Soal Integral
Soal 1.
Jika diketahui ∫ (2x + 1) (x – 5) dx
Maka berapa integralnya …
Jawab:
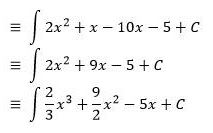
Soal 2.
Jika diketahui ∫ 8x3 – 3x2 + x + 5 dx
Maka berapa integralnya …
Jawab:
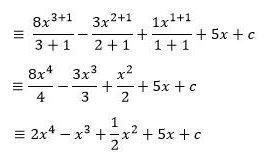
Soal 3.
Jika diketahui 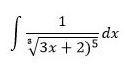
Maka berapa integralnya …
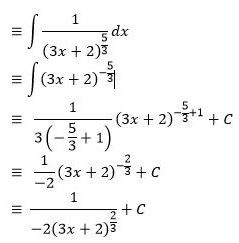
Menentukan Persamaan Kurva
Persamaan garis singgung kurva dan gradien dalam suatu titik, jika y = f(x), maka gradien garis singgung kurva di titik sembarang kurva ialah y’ = f’(x).
Oleh sebab itu, jika gradien singgungnya sudah diketahui, maka kamu bisa mencari persamaan kurvanya dengan cara sebagai berikut:
y = ∫ f ‘ (x) dx = f(x) + c
Jika kamu sudah mengetahui salah satu titik yang melewati kurva, maka nilai c bisa diketahui. Dengan begitu nilai kurvanya akan dengan mudah ditentukan.
Contoh 1.
Jika diketahui turunan y = f(x) = f’(x) = 2x + 3
Dan kurva y = f(x) melewati titik (1,6), maka cari persamaan kurvanya.
Jawab:
f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.
Karena kurva melewati titik (1,6), maka (1) = 6, jadi bisa ditentukan jika nilai C adalah 1 + 3 + c = 6 ↔ c = 2.
Maka, persamaan kurvanya adalah:
Y = f(x) = x2 + 3x + 2.
Contoh 2.
Diketahui gradien garis singgung kurva pada titik (x.y) adalah 2x – 7. Jika kurva tersebut melewati titik (4, -2), tentukanlah persamaan kurvanya.
Jawab:
f ‘(x) = = 2x – 7
y = f(x) = ʃ (2x – 7) dx = x2 – 7x + c.
Karena kurva melewati titik (4, –2)
maka:
f(4) = –2 ↔ 42 – 7(4) + c = –2
–12 + c = –2
c = 10
Jadi bisa diketahui jika persamaan kurva di atas adalah:
y = x2 – 7x + 10.
Tidak sesulit yang dibayangkan bukan? Kamu bisa terus mengasah ilmumu dengan memperbanyak mengerjakan contoh-contoh soal tentang integral tak tentu dan integral trigonometri.
Tips lain biar kamu makin jago dengan soal-soal integral tak tentu maupun integral trigonometri adalah, dengan memperbanyak eksplor rumus integral. Sebut saja rumus integral trigonometri yang tersedia dalam beberapa bentuk.
Nah, kamu bisa mencoba setiap rumus untuk mengerjakan suatu soal. Nantinya, kamu akan paham rumus mana yang paling sesuai dan mudah diaplikasikan.
Integral Tentu
Luas bidang yang mempunyai bentuk tertentu laiknya segitiga, lingkaran, dan segi empat bisa ditentukan menggunakan rumus dasar yang telah diketahui. Yang mana rumus untuk mencari luas bidang dengan terstruktur sudah tersedia lengkap.
Begitu juga dengan keliling bidang tersebut yang bisa ditemukan dengan mudah. Seperti keliling irisan lingkaran yang sudah dibahas pada materi sebelumnya.
Akan tetapi, kamu pasti akan sangat kesulitan untuk menentukan luas dari bidang yang tidak beraturan. Seperti pada gambar berikut dimana luasan area di bagian bawah grafik y = f (x) dibatasi x = a serta x = b dan juga garis x. Nah, luas daerah itu hampir mendekati luas 11 persegi panjang.
Ini gambarnya!
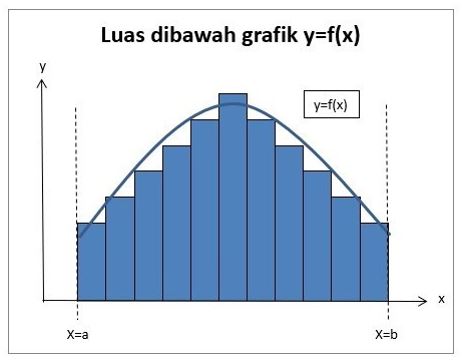
Apabila jumlah dari persegi panjang ditambah lagi menjadi 21 buah seperti di gambar ini!
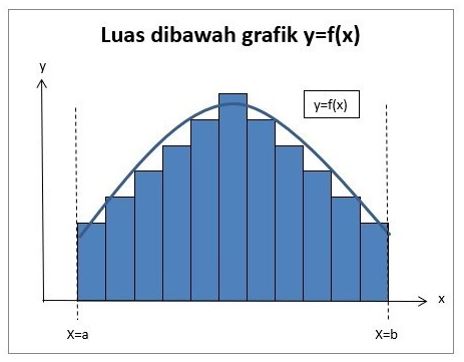
Maka, total luasnya akan semakin mendekati dengan luas daerah grafik yang sudah ditentukan. Jadi, untuk memeroleh luas daerah itu, jumlah dari persegi panjang akan dibuat mendekati “tak terhingga”. Sehingga, kesimpulannya adalah luas daerah tersebut sama dengan limit dari luas total persegi panjang yang menuju ke tak terhingga.
Konsep tersebut jadi dasar dalam mencari luas bidang tak tentu. Dimana luas bidang pada bagian bawah grafik y = f (x) yang juga dibatasi x = a serta x = b bisa dicari dengan cara mengintegralkan fungsi ini di selang a < x < b. Sehingga bisa ditulis menjadi:
![]()
Jadi, bisa dibilang kalai operasi pada integral tentu tidak berbeda dengan integral tak tentu. Namun, nilai a dan b harus disubstitusikan pada fungsi hasil integral menjadi:
![]()
Untuk lebih memahami konsep tersebut, kamu bisa lihat contohnya di bawah ini!
![]()
Atau, bisa juga melihat contoh selanjutnya:
![]()
Sifat Penting Integral Tentu
Rumus yang mendasari integral tentu adalah rumus luas daerah yang dibatasi kurva f(x), x =a, serta x = b dan juga cumbu –x. Dimana salah satu penggunaan integral tentu adalah untuk mencari luas daerah pada bagian bawah kurva.
Ada beberapa sifat penting integral tentu yang bisa kamu pakai pada pengoperasian matematika, diantaranya:

Integral tetap tidak selamanya bisa dikerjakan menggunakan rumus dasar ini ![]() . Penggunaan rumus ditentukan dari bentuk fungsi yang akan diintegralkan. Nah, untuk tekniknya sendiri ada dua jenis, meliputi metode substitusi dan parsial.
. Penggunaan rumus ditentukan dari bentuk fungsi yang akan diintegralkan. Nah, untuk tekniknya sendiri ada dua jenis, meliputi metode substitusi dan parsial.
Contoh Soal Integral Tentu
Biar kamu lebih semangat lagi, silakan simak contoh soal berikut ini, ya!
Tentukan nilai dari fungsi y = f(x) jika fI(x) = x2 – 4 serta f (3) = 5.
Jawab:
Pertama, kamu integralkan dulu fI, menjadi:
fI (x) = x2 – 4
f (x) = ∫ x2 – 4 dx
f (x) = 1/3 x3 – 4x + c
Lalu, substitusikan f(3) = 5 ke dalam persamaan tersebut:
1/3 (3)3 – 4 (3) + c = 5
9 – 12 + c = 5
c = 8
Sehingga, fungsi persamaannya menjadi f (x) = 1/3 x3 – 4x + 8
Penggunaan Integral
Integral bisa digunakan saat menari luas bidang di interval a < x < b serta dibatasi menggunakan sumbu x seperti pada integral tentu. Nah, penggunaan integral sendiri ada berbagai jenis. Mari kita ulas lebih lanjut!
Jenis Kegunaan Integral:
- Untuk luas grafik dengan batasannya adalah grafik f (x), a < x < b dan juga sumbu x. Nah, luasnya sendiri bisa dicari menggunakan rumus
 Dengan catatan bahwa luas bidang ada pada bagian atas sumbu x ataupun pada bagian bawah sumbu x.
Dengan catatan bahwa luas bidang ada pada bagian atas sumbu x ataupun pada bagian bawah sumbu x. - Untuk luas antara dua grafik dengan batasan berupa grafik f (x), grafik g (x) dan a < x < Rumus luasnya menjadi
 . Dengan catatan bahwa f(x) > g(x) di selang a < x < b.
. Dengan catatan bahwa f(x) > g(x) di selang a < x < b. - Untuk luas diantara dua grafik yang memiliki ordo maksimal sejumlah 2. Batasannya berupa grafik f (x) dan grafik g(x). Rumusnya adalah
 . Untuk determinannya atau D didapatkan dari f(x) = g (x) menjadi ax2 + bx + C = 0.
. Untuk determinannya atau D didapatkan dari f(x) = g (x) menjadi ax2 + bx + C = 0.
Penggunaan integral yang lebih lanjut adalah untuk mencari volume. Dimana volume ini adalah suatu bidang yang mengelilingi atau berputar di suatu sumbu. Untuk menghitung volume benda putar, maka digunakan metode kulit dan cakram. Berikut ulasannya!
Metode Kulit
Metode ini dapat digunakan untuk jenis volume grafik dimana batasan bidangnya adalah grafik f(x), sumbu x, dimana a < x < b dengan sumbu putar adalah sumbu y. Sehingga dihasilkan rumus volume V = ![]() .
.
Kedua, bisa dipakai untuk mencari volume antara dua grafik dengan batasan bidang berupa grafik f (x), g (x), serta a < x < b. Sumbu putarnya adalah y, maka rumusnya menjadi V = ![]() .
.
Metode Cakram
Metode cakram adalah penggunaan integral yang bisa diterapkan untuk mencari volume grafik dengan sumbu putar x maupun y. Untuk sumbu putar x dengan batasan bidang berupa grafik f (x), a < x < b, serta sumbu x, menggunakan rumus V = ![]() . Sedangkan untuk sumbu putar y dengan batasan bidang berupa f (x), a < x < b, serta sumbu y, rumus volumenya menjadi V =
. Sedangkan untuk sumbu putar y dengan batasan bidang berupa f (x), a < x < b, serta sumbu y, rumus volumenya menjadi V = ![]() .
.
Metode ini juga dapat digunakan untuk mencari volume antara dua grafik melalui sumbu x dan y. Untuk sumbu putar x dengan batasan grafik f(x), g(x), dan a < x < b, maka dihasilkan rumus V = ![]() . Sedangkan pada sumbu putar y dengan batasan berupa grafik f(x), g(y), dan a < y < b menggunakan rumus volume V =
. Sedangkan pada sumbu putar y dengan batasan berupa grafik f(x), g(y), dan a < y < b menggunakan rumus volume V = ![]() .
.
Contoh Soal Penggunaan Integral
Agar kamu lebih memahami materi ini, maka coba simak baik-baik contoh soal berikut ini!
Tentukan luas dari daerah yang dibatasi 2 grafik y = 2x3 + x2 – x -1 serta y = x3 + 2x2 – x -1!
Jawab:
Buat persamaan f (x) – g (x) dari grafik tersebut untuk memeroleh titik potong, menjadi:
2x3 + x2 – x -1 = x3 + 2x2 – x -1
x3 – x2 – 6x = 0
(x + 2) (X) (x – 3) = 0
Akar yang dihasilkan adalah titik potong dari dua grafik tersebut, yakni x = -2, x = 0, serta x = 3.
Sehingga, luas grafiknya menjadi:

Bisa kamu lihat jika -63/4 mempunyai tanda negatif (-) sehingga bisa diartikan interval 0 < x < 3 dan kurva g (x) > f (x), jadi, penulisan integralnya jadi terbalik. Padahal, semestinya g(x) – f(x). Dimana luasnya tidak mungkin negatif. Jadi, yang dijumlahkan yakni 63/4 menjadi:
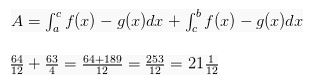
Nah, itulah contoh soal penggunaan integral. Pastinya, kamu bisa mencari soal lainnya agar semakin paham dengan materi integral tentu dan penggunaan integral. Perhatikan setiap poin yang sudah dibahas tersebut dan juga contoh soalnya.
Kamu juga bisa mencoba banyak soal cerita dengan kasus berbeda, sehingga rumus yang sudah diterangkan di atas bisa kamu maksimalkan. Semoga bermanfaat, tetap semangat untuk belajar matematika

