Barisan dan Deret – Pernahkah kamu mendengar baris atau barisan? Mungkin yang lebih sering didenger adalah berbaris ya? Ketika mendengar perintah berbaris, apa yang akan kamu lakukan? Pasti berdiri tegak dengan kawan-kawan lainnya dengan membentuk suatu garis yang rapi bukan?
Misalkan saja berbaris keti upacara bendera, pasti kamu diperintahkan untuk berbaris sesuai dengan kelas masing-masing bukan? Nah, sama halnya dnegan barisan pada materi matematika kali ini, barisan dari suatu bilangan haruslah didasari dengan aturan atau pola tertentu. Supaya lebih jelas, langsung simak saja materi baris dan deret di bawah ini.
Barisan
Pengertian Barisan
Perhatikan barisan bilangan di bawah ini:
- 1,2,3,4,5,6,…. Merupakan barisan bilangan asli
- 1,3,5,7,9,…… Merupakan barisan bilangan asli ganjil
Maka, dari uraian di atas bisa disimpulkan bahwa pengertian barisan adalah susuan suatu bilangan yang dilandasi dengan suatu aturan tertentu. Bilangan yang membentuk suatu barisan disebut suku-suku barisan dan dinotasikan dengan u. Bilangan atau suku pertama dilambangkan u1 hingga akhirnya sampai suku ke-n atau un (dengan n bilangan asli). Perhatikan dengan seksama gambar di bawah ini:
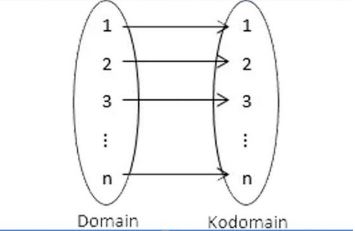
Selain itu, barisan juga bisa diartikan menjadi fungsi dari suatu bilangan asli atau fungsi dimana domainnya adalah himpunan bilangan asli. Sehingga diperoleh Un= f(n).
Agar lebih bisa memahami pengertian barisan, yuk perhatikan contoh persoalan barisan di bawah ini!
Diketahui: Un = (3n + 2), maka suku ke-5 dari barisan itu adalah
U5= (3(5) + 2)= 17.
Barisan Aritmatika
Pengertian barisan aritmatika adalah suatu baris yang mana suku-sukunya diperoleh dari penambahan maupun pengurangan dari suku sebelumnya dengan bilangan b.
Maka: Un – U(n-1) = b
Sebagai salah satu contohnya yaitu 1, 4, 7, 10, 13 adalah baris aritmatika dengan nilai:
b = (13-10) = (10-7) = (7-4) = (4-1) = 3
guna mengetahui nilai suku ke-n dari suatu barisan aritmatika , dapat diketahui dengan cara mengetahui terlebih dahulu nilai suke ke- k serta selisih antar suku yang saling berdekatan atau b. Adapun rumus yang dapat diterapkan yaitu:
Un = Uk+ (n-k)b
Suku pertama dalam suatu baris aritmatika disebut “a” dan selisih antar suku disebut (b), sehingga nilai k=1 dan nilai Un yaitu:
Un= a +(n-1)b , b adalah beda
Suku Tengah Barisan Aritmatika
Jika suatu barisan aritmatika memiliki jumlah suku sebanyak (n) ganjil, dengan suku pertama a serta suku terakhir Un sehingga suku tengah Ut, diperoleh rumus:
Ut = ½(a+Un)
t = ½ (n+1)
Sisipan pada Barisan Aritmatika
Jika diantara dua suku barisan aritmatika disisipkan suku barisan sebanyak k buah sehingga terbentuk suatu barisan aritmatika baru. Jadi, b atau perbedaan akan berubah ketika sudah disisipkan. Beda dari barisan ketika sudah sisiplan yaitu:
b’ =b/(k+1)
dengan:
b’ = beda barisan aritmatika setelah disisipi k buah suku
k = banyaknya suku yang disispkan
Banyaknya suku dalam suatu barisan (n) juga akan berubah ketika sesudah disisipkan, yaitu menjadi:
n’= n+(n-1)k
dengan:
n’= banyaknya suku barisan aritmatika baru
n= banyaknya suku barisan aritmatika lama
Deret
Pengertian Deret
Deret adalah suatu penjumlahan dari anggota atau suku sebuah barisan.
Contohnya:
- 2+4+6+8+10
- 1+3+5+7+11+13
- 2+6+4+12+22
Deret Aritmatika
Pengertian deret aritmatika adalah suatu penjumlah dari semua anggita atau suku-suku sebuah barisan aritmatika. Hasil penjumlahan dari dari suku pertama hingga suku terakhir atau Un barisan aritmatika dapat dihitung dengan:
Sn= U1+U2+U3+U4+ …… +U(n-1) atau
Sn = a+ (a+b)+ (a+2b)+ (a+3b)+ ……+ (a+(n-2)b)+ (a+(n-1)b)
Jika diketahui suku pertama atau a serta nilai Un, maka nilai deret aritmatika yaitu:
Sn= n/2(a+Un)
Namun jika yang diketahui nilai dari Sn maka untuk mencari Un dapat menggunakan persamaan:
Sn-S(n-1) = Un atau Un= Sn-S(n-1)
Barisan Geometri
Pengertian barisan geometri adalah barisan dengan pembanding antara suku yang satu denga suku lain yang saling berurutan dan bersifat tetap. Pembanding dari kedua suku yang berurutab tersebut disebut rasio dan dilambangkan dengan huruf r. Adapun rumus rasio yaitu:
r = sedangkan untuk rumus suku ke-n dari suatu barisan geometri yaitu Un= arn-1
keterangan:
Un = suku ken dari suatu barisan.
a = suku pertama dari suatu barisan.
r = rasio.
n = banyaknya suku dalam suatu barisan.
Suku Tengah Barisan Geometri
Bila suatu barisan geometri mempunya jumlah suku sebanyak (n) ganjil, dengan suku pertama a serta suku terakhir Un, maka suku tengah disebut Ut dari barisan tersebut yakni sebagai berikut:
Rumus suku tengah atau Ut dari suat barisan geometri :
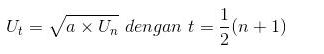
Sisipan pada Barisan Geometri
Jika antara dua suku barisan geometri disisipkan sebanyak k buah suku, maka akan terbentuk suatu barisan geometri yang baru, termasuk juga rasio pada barisan tersebut akan berubah setelah disisipkan k buah suku.
Rasio barisan geometri yang berubah setelah disisipkan k buah suku yaitu akan menjadi:
![]()
Keterangan:
r’ = rasio barisan geometri yang berubah setelah disisipkan k buah suku.
K = banyaknya suku yang disisipkan dalam barisan geometri.
Selanjutnya, untuk banyaknya suku dari barisan geometri yang telah disisipkan k buah suka juga akan mengalami perubahan, menjadi:
n’ = n+(n-1)k
keterangan:
n’ = banyaknya jumlah suku barisan geometri yang baru setelah disisipkan k buah suku.
n = banyaknya suku barisna geometri lama, sebelum disisipkan k buah suku.
Deret Geometri
Setelah memahami barisan geometri, maka ada juga yang namanya deret geometri. Apa itu deret geometri? Pengertian deret geometri adalah jumlah dari pada suku-suku suatu barisan geometri. Deret geometri pada n suku pertama dilambangkan dengan Sn dan memiliki beberapa rumus di bawah ini:
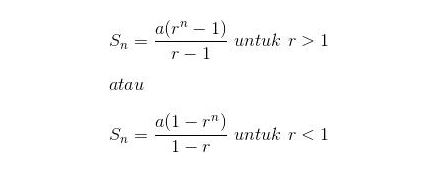
keterangan:
Sn = jumlah n pada suku pertama
a = suku pertama
r = rasio
n = banyaknya suku
Deret Geometri Tak Berhingga
Suatu barisan geometri yang memiliki rasio antar -1 dan 1 disebut sebagai barisan geometri konvergen. Deret geomertri dari suatu barisan geometri konvergen dan banyaknya suku yang tak berhingga dapat dihitung menggunakan rumus berikut ini:
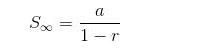
keterangan:
a = suku pertama dari barisan
r = rasio barisan geometri konvergen dengan syarat antara -1 dan 1.
Hubungan Barisan dan Deret
Hubungan antar barisan dan deret dapat diungkapkan menggunakan rumus:
Un= Sn-Sn-1
Beda pada barisan aritmatika dapat kamu diperoleh dari turunan dua deret aritmatika.
Contoh Soal Barisan dan Deret
Nah, setelah memahami materi barisan dan deret di atas, yuk perhatikan contoh soal di bawah ini, perhatikan baik-baik, kurangi ngelamun ya hehe
- Suku ke-10 dari barisan 2, 6, 10, 14, 18 ….yaitu…
Jawab:
a = 2
b = 4
suku ke 10 = U10
Un = a+(n-1)b
U10 = 2 + (10-1)4
U10 = 2+ 9.4
U10 = 2+36
U10 = 38
- Tentukan suku Un ke 10 dari barisan geometri 1,3,9,27……
Jawab:
Diketahui :
r = 9:3 = 3 :1 = 3
a = 1
Un = arn-1
U10 = 1.3(10-1)
U10 = 1.37
U10 = 1. 19.683
Jadi U10 dari barisan geometri di atas adalah 19.683
Jadi itulah, materi barisan dan deret, baik aritmatika maupun geometri. Kedunya memiliki sifat serta rumus masing-masing namun saling berkaitan. Semoga contoh soal barisan dan deret aritmatika dan geometri dan penyelesaiannya dapat membantumu dalam belajar. Semangat belajar ya!

