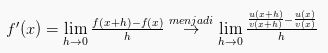Turunan Fungsi Aljabar

Dalam matematika, ilmu aljabar mengambil peran yang cukup besar. Selain fungsi aljabar, saat duduk di bangku SMA, kamu juga akan disuguhi dengan materi turunan fungsi aljabar.

Secara umum, turunan merupakan pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang telah dimasukkan. Dalam bahasa lain, turunan dapat menunjukan suatu besaran berubah karena perubahan besaran lain. Proses untuk menemukan turunan ini disebut dengan diferensisasi.

Konsep turunan sendiri sebenarnya sangat sering diterapkan dalam kehidupan sehari-hari, baik dalam ilmu matematika maupun yang lainnya.

Dalam ilmu matematika, fungsi turunan sering digunakan untuk menghitung garis singgung pada sebuah kurva maupun untuk menghitung kecepatan. Sementara pada bidang ilmu lain, konsep turunan sering diaplikasikan untuk mencari laju pertumbuhan organisme (biologi), laju pemissahan (kimia), kepadatan kawat (fisika), dan keuntungan marjinal (ekonomi).

Seluruh fungsi di atas sebenarnya memiliki konsep yang sama, yakni konsep turunan. Materi selengkapnya tentang turunan fungsi aljabar bisa kamu simak di bawah ini ya.

Pengertian Turunan Fungsi Aljabar

Turunan fungsi aljabar merupakan proses turunan dari suatu fungsi ke fungsi selanjutnya. Contoh sederhananya, fungsi f yang menjadi f’ dan memiliki nilai tak beraturan.

Misalan lain, pada fungsi y = f(x), maka turunan dari variabel y pada variabel x bisa dinotasikan dengan atau y’ yang bisa didefinisikan menjadi:

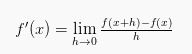
Aturan Menentukan Turunan Fungsi

Tanpa melalui proses limit kamu bisa menentukan turunan. Namun, untuk kebutuhan ini, pernyataan mengenai turunan dasar, turunan operasi aljabar pada dua fungsi, turunan fungsi invesr dan aturan rantai turunan fungsi komposisi dibutuhkan.

Berikut ini informasi lengkapnya:

Turunan Dasar

Aturan untuk menentukan turunan dasar, antara lain adalah:

1. F(x), akan menjadi f’(x) = 0
2. Apabila f(x) = x, maka f’(x) = 1
3. Aturan pangkat akan berlaku apabila f(x) = xⁿ, berarti f’(x) = n X ^n-1
4. Aturan kelipatan konstanta akan berlaku apabila (kf) (x) = k * f’(x)
5. Aturan rantai akan berlaku apabila (f o g) (x) = f’ (g (x)) = f’ (g(x)) * g’(x))

Turunan Jumlah, Selisih, Hasil Kali, dan Hasil Bagi Dua Fungsi

Contohnya ialah fungsi d dan g yang terdiferensialkan pada selang I, maka didapatkan fungsi f + g, f – g, fg, f/g, (g (x)  ≠  0 pada I), yang terdiferensialkan pada I dengan menggunakan aturan berikut:

1. ( f + g )’ (x) = f’ (x) + g’ (x)
2. ( f – g )’ (x) = f’ (x) – g’ (x)
3. (fg)’ (x) = f’(x) g(x) + g’(x) f(x)
4. ((f)/g )’ (x) = (g(x) f’ (x)- f(x) g’ (x))/((g(x)²)

Turunan Fungsi Trigonometri

Aturan yang perlu diperhatikan adalah:

1. d/dx ( sin x ) = cos x
2. d/dx ( cos x ) = – sin x
3. d/dx ( tan x ) = sec² x
4. d/dx ( cot x ) = – csc² x
5. d/dx ( sec x ) = sec x tan x
6. d/dx ( csc x ) = -csc x cot x

Turunan Fungsi Invers

Aturannya ialah: (f^-1)(y) = 1/(f’ (x)), atau dy/dx 1/(dx/dy)

Rumus-rumus Turunan Fungsi Aljabar

Setelah mengetahui pengertian atau definisi dari turunan fungsi aljabar, selanjutnya kamu bisa mengenal rumus-rumus turunan fungsi aljabar. Melalui rumus-rumus ini, kamu bisa mencari penyelesaian dalam sebuah masalah yang berkaitan dengan fungsi alajabar.

Rumus turunan fungsi alajabr sendiri terdiri dari fungsi pangkat f(x) = xⁿ. Dimana hasil kali fungsi f(x) = u(x), v (x), hasil pembagian fungsi  serta pangkat fungsi f(x) = (u (x))ⁿ

1. Rumus  Turunan Fungsi Pangkat f(x) = xⁿ

Untuk menyelesaikan soal dengan bentuk pangkat turunan, kamu bisa menggunakan rumus  sebagai:

Jadi, bisa disimpulkan jika rumus akhir dari turunan fungsi pangkat ialah:

f’(x) = nx^n-1

2. Rumus Turunan Hasil Kali Fungsi f(x) = u(x) ^. v (x)

Apabila didapati turunan yang merupakan hasil kali fungsi u(x) serta v(x), maka turunanan bisa diperoleh dengan:

Jadi, rumus akhir yang bisa kamu pakai untuk menyelesaikan turunan fungsi aljabar hasil perkalian ialah

f’(x) = u’ v + w’

3. Rumus Turunan Fungsi Pembagian

Sehingga didapatkan

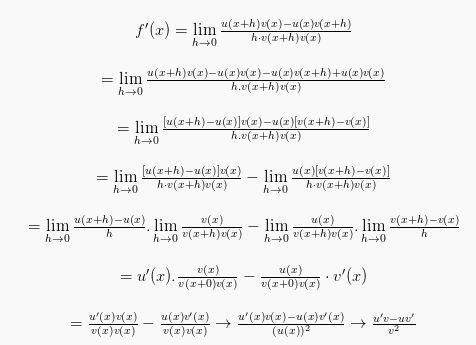
Jadi, rumus akhir yang bisa digunakan adalah:

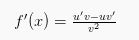
4. Rumus Turunan Pangkat dari Fungsi f(x) = (u(x))ⁿ

Sebelumnya, kamu perlu mengingat jika f(x) = xⁿ maka akan didapatkan:

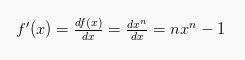
Karena f(x) = (u(x))ⁿ = uⁿ, maka:

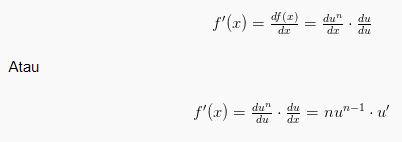
4. Rumus Turunan Trigonometri

Selain bisa menghasilkan rumus turunan fungsi aljabar itu sendiri, definisi turunan juga menunjukkan terbentuknya rumus turunan trigonometri, yakni: (u dan v masing-masing merupakan fungsi dari ), antara lain: y’

• y = sin x → y’ – cos x
• y = cos x →  y’ = -sin x
• y = tan x →  y’ = sec² x
• y = cot x →  y’ = csc² x
• y = sec x →  y’
• y = csc x →  y’ = csc * cot x
• y = cosⁿ x →  y’ = -n cos^n-1 * sin x
• y = sin u →  y’ = u’ cos u
• y = cos u →  y’ = u’ cos u
• y = cos u →  y’ = u’ sin u
• y = tan u →  y’ = ui sec² u
• y = cot u →  y’ = -u csc² u
• y = sec u → y’ = u’ sec u tan u
• y = csc u → y’ = u’ csc u cot u
• y = sinⁿ  u → y’ = n.u’ sin^n-1 cos u
• y = cosⁿu → y’ = -n.u’  cos^n-1 . sin

Contoh Soal

Soal 1.

Tentukan turunan f(x) =

f(x) = (2x + 1)⁴

Jawab:

Misalnya:

U(x) = 2x +1 → u’ (x) = 2

n = 4

f’ (x) = n [u(x)]^n-1 * u’ (x)

f’ (x) = 4(2x)^4-1 * 2

f’ (x) = 8(2x + 1)³

Soal 2.

Tentukan turunan fungsi f(x) = 2 (x4 – 5)

Jawab:

Misal jika u(x) = 2 dan v(x) = x4 – 5, maka didapatkan:

U’ (x) = 2 dan v’ (x), berarti 4*3

Dengan demikian, bisa didapatkan penjabaran dan hasilnya sebagai berikut:

f’ (x) = u’(x) * v(x) + u(x) * v(x) = 2(x4 – 5) + 2x(4 * 3) = 2 * 4 – 10 + 8 * 4 = 10 * 4 – 10

Soal 3.

Turunan fungsi pertama f(x) =  yakni…

Jawab:

Soal tersebut merupakn persoalan fungsi dalam bentuk y’ = auⁿ  yang bisa dibahas dan diselesaikan menggunakan rumus y’ = n * a * u^n-1  Maka diperoleh

Sehingga turunan yang didapatkan ialah

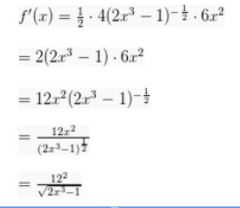
Bagaimana, tidak sesulit yang dibayangkan bukan? Setelah kamu memahami aturan-aturan pada turunan fungsi, dan menghafal rumus-rumus yang bisa digunakan, maka soal tentang turunan fungsi bisa diselesaikan dengan mudah.

Tentunya untuk menambah wawasan dan keahlian, kamu harus aktif mencari contoh-contoh soal lain dan mengerjakannya sesuai rumus yang benar.

Selamat belajar!