Materi Irisan Dua Lingkaran

Irisan Dua lingkaran – Materi lingkaran dalam pelajaran matematika bisa dikatakan sebagai salah satu materi paling rumit. Di samping banyaknya rumus yang harus kamu hafalkan, banyak teori perhitungan yang harus diselesaikan dengan metode khusus.

Seperti pada materi sebelumnya, yang mana kamu sudah mempelajari materi persamaan lingkaran, disini kamu juga akan kembali disuguhi rumus-rumus yang siap membuat logikamu berfikir keras.

Jika sebuah lingkaran saling memotong, maka akan membentuk daerah irisan. Nah, inilah yang disebut dengan irisan lingkaran. Materi kali ini, kamu akan mempelajari tentang bagaimana cara mencari keliling irisan dua lingkaran. Hal dasar yang mesti kamu tahu adalah tentang luas juring dan panjang busur.

Pada materi irisan lingkaran ini, kamu juga harus sedikit flashback ke materi tentang kosinus agar bisa menentukan besar sudut. Selain itu, dengan aturan kosinus, kamu bisa menentukan jarak antara dua titik.

Siap untuk menerima materinya? Yuk, simak ulasannya di bawah ini!

Kedudukan atau Sifat Irisan Dua Lingkaran

Sebelum masuk ke rumusnya, sebaiknya, kamu simak dulu beberapa kedudukan antara irisan dua lingkaran. Setelah kamu paham, maka akan lebih mudah memahami materi irisan lingkaran ini.

1. Lingkaran Berpotongan

Apabila jarak antara dua titik pusat lingkaran adalah P₁P₂ < r₁r₂, maka, irisan dua lingkaran tersebut akan ada pada posisi saling berpotongan.

2. Lingkaran Bersinggungan Luar

Irisan dua lingkaran akan disebut saling bersinggungan di luar apabila jarak titik pusat keduanya adalah P₁P₂ = r₁r₂.

3. Lingkaran Bersinggungan Dalam

Irisan dua lingkaran akan disebut saling bersinggungan dalam apabila jarak dua titik pusatnya adalah P₁P₂ = |r₁r_2|.

4. Tidak Bersinggungan

Irisan dua lingkaran disebut tidak saling bersinggungan di luar apabila jarak titik pusat keduanya adalah P₁P₂ > r₁r_2.. Apabila jarak dua titik pusat lingkaran adalah P₁P₂ = 0 atau P₁ tidak sama dengan P₂, dan r₁ < r₁, maka bisa dibilang tidak saling bersinggungan di dalam.

Jadi, bisa dibilang kalau jarang dua titik pusat lingkaran adalah nol, maka lingkaran tersebut tidak saling bersinggungan. Irisan dua lingkaran juga tidak bisa bersinggungan apabila satu lingkaran ada di dalam lingkaran lainnya.

Agar lebih jelas,  silakan kamu lihat gambar di bawah ini!

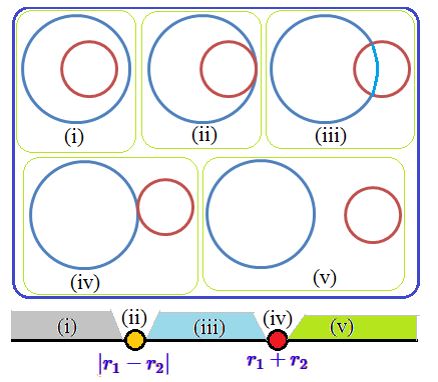
Garis Singgung Persekutuan Lingkaran

Pada irisan lingkaran dikenal juga adanya garis singgung lingkaran. Yang mana garis ini menyinggung lingkaran pada suatu titik serta berpotongan secara tegak lurus dengan jari-jari pada titik singgungnya. Kuadrat jarak diantara titik pusat dua lingkaran yang dikurangkan dengan kuadrat jumlah panjang jari-jari lingkaran disini sama dengan kuadrat panjang garis singgung persekutuan dalam lingkaran.

Seperti yang sudah dibahas sebelumnya bahwa ada garis yang bersinggungan di dalam dan di luar lingkaran. Maka dari itu, ada dua rumus yang harus kamu ketahui.

Untuk panjang garis singgung persekutuan yang ada di dalam lingkaran, rumusnya adalah:

Sedangkan untuk panjang garis singgung persekutuan yang ada di luar lingkaran, rumusnya adalah:

Keterangan:

d => panjang dari garis singgung

p => jarak dua titik pusat

R => jari-jari lingkaran yang lebih besar

r => jari-jari lingkaran yang lebih kecil

Jika kamu sudah mengetahui rumus dari panjang garis singgung lingkaran, sekarang kita akan masuk ke luas dan keliling irisan lingkaran. Langsung saja, check these out!

Luas dan Keliling Irisan Dua Lingkaran

Untuk bisa menentukan keliling irisan lingkaran, kamu harus lebih dulu menentukan panjang busur kedua lingkaran tersebut. Sebelumnya, coba kamu lihat gambar di bawah ini!

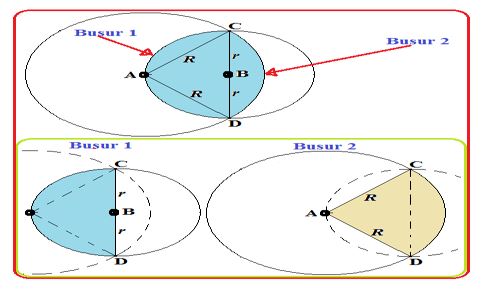
Cara menghitung keliling irisan lingkaran berdasarkan gambar tersebut adalah :

1. Menentukan busur 1 lingkaran yang pertama disimbolkan dengan L1. Rumusnya adalah sebagai berikut : L1 = <CAD/360^o . 2π . r
2. Menentukan busur ke dua di lingkaran kedua atau L2, rumusnya adalah sebagai berikut : L2 = <CBD/360^o . 2π . r

Jadi, keliling irisan lingkaran tersebut adalah busur 1 + busur 2, rumusnya menjadi :

3. Keliling irisan lingkaran = <CAD/360^o . 2π . r + <CBD/360^o . 2π . r

Setelah kamu tahu rumus untuk mengetahui keliling irisan lingkaran, kamu juga perlu mengetahui cara mencari besar sudutnya. Nah, untuk mengetahui besar sudut masing-masing busur, kamu dapat memakai aturan kosinus. Semisal, untuk mencari besar sudut CAD di busur yang pertama, kamu harus menerapkan :

cos <CAD = AD² + AC² – CD²

2. AD. AC

= r² + r² – CD²

2. r. r

= 2r² – CD²

2r²

Jika sudah, kamu juga perlu mengetahui cara menentukan panjang garis CD. Namun, sebelumnya, tentukan dulu titik C serta D (titik potong dua lingkaran) dahulu. Caranya, dengan memakai konsep jarak antara dua titik. Semisal titik C (x₁, y₁) serta D pada titik (x₂, y₂). Maka, panjang dari CD adalah :

CD = √(x₂ – x₁)² + (y₂ – y₁)²

Hal yang perlu kamu perhatikan, ketika akan menentukan keliling dari suatu irisan lingkaran, maka langkah-langkah yang perlu kamu lakukan diantaranya :

1. Tentukan titik potong dua lingkaran tersebut.
2. Kemudian, tentukan panjang garis CD.
3. Setelah itu, tentukan sudut dari dua busur lingkaran.
4. Lalu, jumlahkan panjang dua busur lingkaran.

Contoh Soal Keliling Irisan Dua Lingkaran

Gimana kalau kita langsung saja mengerjakan soal supaya pemahaman terkait irisan lingkaran ini semakin paripurna. Nah, berikut adalah contohnya!

Contoh Soal 1

Carilah berapa keliling irisan dua lingkaran ini! L1 => (x + 2)² + (y – 1)² = 49, kemudian L2 => (x – 6)² + (y – 1)² = 9

Jawab :

Pertama-tama, kamu gambar dulu irisan dua lingkaran tersebut. Lalu, tentukan titik potong dua lingkaran, yakni:

L1 => (x + 2)² + (y – 1)² = 49

x² + y² + 4x – 2y – 44 =0

L2 => (x – 6)² + (y – 1)² = 9

x² + y² – 12x – 2y + 28 =0

Lalu, kamu eliminasikan dua persamaan lingkaran tersebut :

x² + y² + 4x – 2y – 44 =0

x² + y² – 12x – 2y + 28 =0 –

16 x – 72 = 0

x = 4,5

Setelah itu, kamu substitusikan nilai dari x = ,5 pada persamaan lingkaran yang ke dua :

(x – 6)² + (y – 1)² = 9

(4,5 – 6)² + (y – 1)² = 9

2,25 – (y – 1)² = 9

(y – 1)² = 6, 75

y – 1 = √6,75

y = 1 + √6,75

y₁ = 1 – √6,75 V y₂ = 1 + √6,75

Jadi, titik potong dua lingkaran adalah C (4, 5 ; 1 – √6,75) serta D (4, 5 ; 1 + √6,75)

Panjang CD jadi = √(4,5 – 4,5)² + [( 1 + √6,75) – (1 – √6,75)]² = 2√6,75

Lalu, kamu tentukan besar sudut dua busur lingkaran. Pada busur lingkaran 1, berlaku :

cos <CAD = (2r² – CD²)/ 2r²

= (2. 7² – (2√6,75)²)/ 2. 7²

= (98 – 27)/98

= 71/98

<CAD         = arc cos 71/98

<CAD         = 43,57^o = 44^o

Kemudian cari busur di lingkaran yang kedua atau L2, caranya:

cos <CBD = (2r² – CD²)/ 2r²

= (2. 3² – (2√6,75)²)/ 2. 3²

= (18 – 27)/18

= -9/18 atau -1/2

<CBD         = arc cos -1/2

<CBD         = 120^o

Panjang busur 1 => <CAD/360^o . 2π. r = 44^o/360^o . 2 22/7. 7 = 5,38

Panjang busur 2 => <CBD/360^o . 2π. r = 120^o/360^o . 2 22/7 .7 = 6,29

Jadi, keliling irisan lingkaran tersebut adalah busur 1 + busur 2 = 5,38 _ 6,29 = 11,67

Masih ada yang belum dipahami? Coba deh untuk banyak mengerjakan soal-soal tentang keliling irisan lingkaran. Cari soal dalam bentuk cerita, kemudian selesaikan dengan rumus dan metode yang sudah dijelaskan di atas.

Demikian pembahasannya, semoga bermanfaat!