Persamaan Lingkaran – Jika kamu memerhatikan roda mobil, tentu dari titik tengah ke sisi-sisi lingkarannya akan mempunyai jarak yang sama. Sebab, lingkaran bisa diartikan sebagai tempat kedudukan titik-titik mempunyai jarak yang sama pada titik tertentu pada bidang datar. Titik dalam hal ini dimaksudkan sebagai pusat lingkaran, sedangkan jarak adalah jari-jari. Nah, setelah kamu tahu apa itu lingkaran, yuk, kita bahas tentang persamaan lingkaran!
Rumus Persamaan Lingkaran
Persamaan lingkaran ada beberapa jenis. Mulai dari persamaan yang terbentuk dari jari-jari dan titik pusat, serta persamaan yang dapat dicari jari-jari dan titik pusatnya. Nah, persamaan umum lingkaran sendiri adalah:
x2 + y2 + Ax + By + C = 0
Dari persamaan tersebut, kamu bisa menentukan titik pusat dan juga jari-jarinya. Berikut rumusnya:
Rumus Pusat Lingkaran
![]()
Sedangkan rumus jari-jari lingkarannya
![]()
Persamaan Lingkaran dengan Pusat P (a, b) dan Jari-jari r
Kalau lingkaran sudah diketahui titik pusat serta jari-jarinya, maka bisa menggunakan rumus persamaan lingkaran berikut ini!
(x – a)2 + (y – b)2 = r2
Dari persamaan itu, kamu bisa menentukan apakah suatu titik ada di dalam lingkaran atau di bagian luarnya. Supaya kamu bisa menentukan letaknya, silakan substitusikan titik di variabel x serta y. Lalu, kamu bandingkan saja hasilnya dengan kuadrat jari-jari.
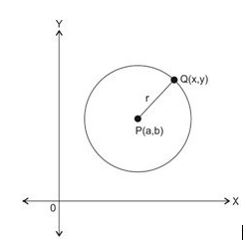
Jika titik M (x1, y1) berada pada lingkaran, maka:
(x1 – a)2 + (y2 – b)2 = r2
Sedangkan apabila titik M tersebut ada di dalam lingkaran, maka:
(x1 – a)2 + (y2 – b)2 < r2
Apabila titik M berada di luar lingkaran, maka:
(x1 – a)2 + (y2 – b)2 < r2
Selain menggunakan rumus persamaan lingkaran di atas, kamu juga bisa mengerjakan soal persamaan lingkaran dengan menggunakan rumus bantu. Berikut rumusnya!
Untuk menentukan titik tengah dari lingkaran, kamu pakai rumus ini:
( (x1 + x2)/2, (y1 + y2)/2
Persamaan Lingkaran dengan Pusat O (0, 0), Jari-jari r
Apabila titik pusat lingkaran terletak pada O (0, 0), maka substitusi di bagian yang sebelumnya adalah:
(x – 0)2 + (y – 0)2 = r =>x2 + y2 = r2
Berdasarkan persamaan tersebut, kamu juga bisa menentukan letak dari titik tertentu pada lingkaran.
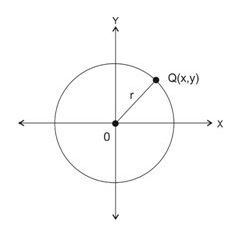
Jika titik M (x1,y1) ada pada lingkaran, maka x12 + y12 = r2
Jika terdapat dalam lingkaran, maka x12 + y12 < r2
Sedangkan, di luar lingkaran, maka x12 + y12 > r2
Apakah kamu masih merasa bingung? Jika iya, pahami dulu contoh soal berikut ini, ya!
Contoh Soal Persamaan Lingkaran
1. Contoh Soal
Suatu lingkaran mempunyai titik pusat (2, 3) serta diameter 8 cm. Coba, cari persamaan lingkaran tersebut!
Pembahasan:
Diketahui diameternya adalah 8, maka, r = ½ . d = ½ . 8 = 4. Persamaan lingkaran yang terbentuk menjadi:
(x – 2)2 + (y – 3)2 = 42
x2 – 4x + 4 + y2 – 6y + 9 = 16
x2 + y2 – 4x – 6y – 3 = 0
Jadi, persamaan lingkaran dari diameter 8 cm dan titik pusat (2, 3) adalah x2 + y2 – 4x – 6y – 3 = 0
2. Contoh Soal
Tentukan pusat serta jari-jari dari persamaan lingkaran ini x2 + y2 – 4x + 6y -3 = 0!
Pembahasan:
Dari persamaan lingkaran tersebut, diketahui bahwa A = -4 dan B = 6, sedangkan C = -3.
Kamu bisa gunakan rumus yang sudah dijelaskan di atas untuk menentukan pusat dan jari-jari lingkarannya.
Pusat => A (a, b) = (-A/2, -B/2) = (- (-4/2), -6/2) = (2, -3)
Sedangkan jari-jarinya adalah => r2 = a2 + b2 – C => r2 = 22 + (-3)2 => r2 = 16, r = 4
Jadi, pusat lingkaran dengan persamaan x2 + y2 – 4x + 6y -3 = 0 adalah (2, -3), sedangkan jari-jarinya adalah 4 cm.
Perpotongan Garis dan Lingkaran
Lingkaran yang memiliki persamaan x2 + y2 – Ax + By + C = 0 juga bisa ditentukan apakah garis h yang mempunyai persamaan y = mx + n itu tidak menyinggung, menyentuh, maupun memotong lingkaran. Caranya, dengan memakai prinsip diskriminan.
Persamaan 1 => x2 + y2 – Ax + By + C = 0
Persamaan 2 => y = mx + n
Substitusikan persamaan 2 pada persamaan 1. Lalu, akan didapatkan bentuk persamaan kuadrat berikut:
x2 + (mx + n)2 – Ax + B (mx + n) + C = 0
Lalu, bandingkan nilai diskriminannya. Dari situ bisa dilihat apakah garis memotong, menyinggung, atau tidak.
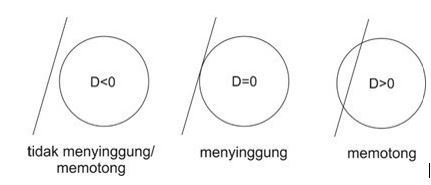
Jika D < 0, maka garis h tidak menyinggung ataupun memotong lingkaran.
Jika D = 0, berarti garis h menyinggung lingkaran.
Jika D > 0, berarti garis h memotong lingkaran.
Biar lebih jelas, coba kamu lihat gambar di bawah ini!
Persamaan Garis Singgung Lingkaran
Garis singgung pada lingkaran tentu akan bertemu tepat dengan satu titik di suatu lingkaran. pada titik pertemuan tersebut, bisa ditentukan persamaan garisnya. Persamaan yang melalui suatu titik P (x1, y1) bisa ditentukan dengan rumus persamaan lingkaran yang sudah dibahas sebelumnya.
x2 + y2 = r2
Maka, persamaan garis singgungnya menjadi: xx1 + yy1 = r2
Untuk bentuk (x – a)2 + (y – b)2 = r2, maka persamaan garis singgungnya menjadi:
(x – a) (x 1 – a) + (y – b) (y1 – b) = r2
Lain lagi dengan bentuk x2 + y2 – Ax + By + C = 0, maka persamaan garis singgungnya menjadi:
xx1 + yy1 + A/2 (x + x1) + B/2 (y + y2) + C = 0
Biar kamu lebih paham, sebaiknya simak contoh soalnya di bawah ini!
Contoh Soal
Pada lingkaran x2 + y2 – 4x + 6y – 12 = 0, persamaan garis singgung pada titik (-1, 1) adalah …
Jawab:
Kamu bisa tahu dari soal tersebut, persamaan lingkarannya adalah x2 + y2 – 4x + 6y – 12 = 0, sehingga, A = -4, B = 6, serta C = -12. Lalu, x1 = -1 dan y1 = 1.
Masukkan angka-angka yang sudah diketahui tersebut pada rumus yang sudah diberikan pada materi.
xx1 + yy1 + A/2 (x + x1) + B/2 (y + y2) + C = 0
x (-1) + y (1) – /2 ( x -1) + 6/2 (y + 1) – 12 = 0
-3x + 4y – 7 = 0
Jadi, persamaan garis singgung dari lingkaran di atas adalah 4y = 3x + 7.
Cukup dulu pembahasan tentang persamaan lingkarannya. Semoga mudah untuk dipahami, ya! Jangan lupa memperbanyak latihan soal agar kamu semakin lincah mengerjakannya. Selamat belajar.

