Memahami Logaritma Itu Mudah! Bonus 5 Contoh Soal dan Pembahasannya

Materi logaritma kelas 10, kamu sudah mempelajari mengenai bilangan eksponen atau bilangan berpangkat. Kali ini, kamu juga akan tau mengenai kebalikan dari eksponen, yakni logaritma. Jadi, kalau pada eksponen, yang dicari adalah hasil pangkat, sebaliknya, pada logaritma, yang dicari adalah besar pangkatnya.

Yuk, bahas bersama agar kamu semakin tahu!

Pengertian Logaritma

Logaritma merupakan kebalikan (invers) dari eksponen atau pemangkatan. Logaritma digunakan supaya kamu bisa menentukan besarnya pangkat dari bilangan pokok tertentu. Secara lebih mudah, logaritma mampu membuat kamu tahu besar pangkat dari bilangan yang sudah diketahui berapa hasil pangkatnya.

Mungkin, kamu akan tahu hasil dari 2 pangkat berapa untuk menghasilkan angka 8. Mudah banget karena hasil pemangkatan adalah bilangan bulat. Nah, kalau contoh soalnya begini, 5 pangkat berapa sehingga menghasilkan 2.236? Wah, pasti kepala mulai oleng, kan?

Maka dari itu, kamu butuh yang namanya logaritma. For your information, kamu tidak cuma bisa menggunakan logaritma untuk matematika saja. Melainkan juga untuk berbagai bidang studi yang lain. Semisal, pada bidang studi kimia, kamu membutuhkan logaritma untuk menentukan orde reaksi. Begitu juga di pelajaran akustik, kamu bisa menentukan koefisien serap bunyi menggunakan logaritma.

Dalam logaritma, prinsip dasarnya bisa kamu lihat di bawah ini!

Apabila ada perpangkatan

a^c=b

Jika perpangkatan ini diubah dalam bentuk logaritma, maka hasilnya

^alog b = c

dengan catatan bahwa a lebih dari nol, dan a tidak sama dengan 1.

Keterangan :

a = basis logaritma

b = bilangan numerus (yang dicari nilai logaritmanya)

c = besar pangkatnya.

Biar lebih paham, coba ,deh, lihat contoh berikut :

1. Pada perpangkatan 3² = 9, bentuk logaritmanya adalah ³log 9 = 2
2. Pada perpangkatan 2³= 8, bentuk logaritmanya adalah ²log 8 = 3
3. Pada perpangkatan 5³= 125, bentuk logaritmanya adalah ⁵log 125 = 3

Ada juga contoh bentuk logaritma yang tidak hanya berbentuk bilangan bulat, melainkan juga berbentuk pecahan.

1. Pada perpangkatan 3^-4 = 1/81, bentuk logaritmanya adalah ³log 1/81 = -4
2. Pada perpangkatan 4^3/2 = 8, bentuk logaritmanya adalah ⁴log 8 = 3/2

So, mudah sekali, kan? Kamu tinggal mengingat bahwa bilangan pokok disebut basis, lokasinya ada sebelum tanda log. Sedangkan numerus atau hasil ada di bawah kata log. Paham, dong? Gampang, ya!

Siap lanjut? Oke!

Sifat Logaritma

Setelah kamu paham tentang prinsip dasarnya, kamu juga wajib banget tahu sifat logaritma. Sebab, sifat logaritma adalah bekal utama untuk mengerjakan soal nantinya. Kalau tidak paham dengan sifat-sifatnya, mustahil bisa mengerjakan!

So, cek sifat-sifat logaritma di bawah ini!

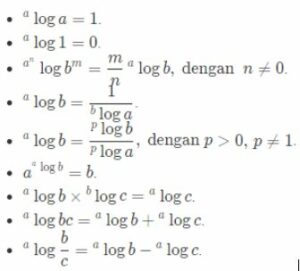
“Wah, banyak banget, nggak seru nih!” Eh, tunggu dulu, kamu hanya perlu memperbanyak mengerjakan contoh-contoh soal logaritma. Dengan begitu, kamu akan bisa menghafal, tanpa effort lebih. Asyik banget, kan? So, langsung saja kita mulai mengerjakan dan membahas soal bareng-bareng. Here we go!

Kumpulan Contoh Soal Logaritma dan Pembahasannya

Langsung saja, kita masuk ke soal nomor 1. Tidak perlu tegang, sebelum membahas soal, kamu bisa mengunyah permen karet biar lebih rilex. Sudah? Yuk, simak contoh soal logaritma dan pembahasannya baik-baik ya!

1. ²log 4 + ²log 8 = …

Pada soal model ini, hal yang harus kamu lakukan pertama kali adalah dengan mengecek basis. Ingat, kan, basis ada dimana? Yak, betul, sebelum kata log. Coba dilihat, keduanya mempunyai nilai basis sama, yakni 2. Jika begitu, kamu bisa memakai sifat logaritma yang ke delapan. Coba cek lagi ke atas!

^alog bc = ^alog b + ^alog c, jadi, penyelesaiannya adalah ²log (4 x 8), hasilnya adalah ²log 32. Pertanyaan selanjutnya adalah 2 pangkat berapa agar hasilnya jadi 32? Yak, betul, jawabannya 5. Yey, kamu berhasil mengerjakan satu soal.

2. ⁸log 32 = …

Soal logaritma nomor 2 will be more easily. Tetapi, kamu tidak akan bisa langsung mengerjakannya. Melainkan harus memperhatikan soal lebih jeli lagi. Untuk itu, kamu bisa menjadikan bilangan 8 dan 32 itu dalam bentuk perpangkatan. 8 adalah 2³, dan 32 adalah 2⁵. Bentuk logaritmanya sekarang bisa kamu ubah menjadi :

3. Jika diketahui ²log 8 = m dan ²log 7 = n, maka nilai ¹⁶log 14, hasilnya adalah …

Contoh soal logaritma ketiga tampak sedikit rumit, tapi, kalau konsepnya sudah dipahami, soal ini cukup mudah, kok. Kamu dapat menyelesaikan soal ini dengan sifat logaritma ke-lima. Sehingga, kamu bisa mengerjakan seperti ini!

Memilih 2 sebagai angka basis dikarenakan angka 2 paling kerap muncul di soal. Angka 2 ada di soal sebanyak 2 kali, 8 hanya 1 kali, dan angka 7 juga 1 kali. Inilah alasan kenapa 2 jadi angka basis. Jika sudah, ubah bentuknya menjadi :

Kalau sudah, uraikan numerusnya, sebaiknya diubah sesuai dengan angka-angka pada soal. Maksudnya, kamu sudah tahu hasil dari ²log 8 dan ²log 7. Dikarenakan numerus yang ada adalah 8 dan 7, maka angka 14 diuraikan jadi 7 x 2 dan 16 jadi 8 x 2. Penyelesaiannya pun menjadi :

²log 7 + ²log 2

²log 8 + ²log 2

n + 1

m + 1

4. ²log (x + 9) = 5, maka nilai x adalah …

Nah, contoh soal logaritma nomor 4 ini akan semakin hot, so, siapkan amunisi berpikir yang lebih kuat! Pada persamaan ini, ruas kanan dapat diubah dalam bentuk logaritma. Caranya, dengan memilih nilai basis yang tidak berbeda dengan ruas bagian kiri. Silakan Anda gunakan sifat ^alog b^c = c^a log b.

²log (x + 9) = 5 x ²log 2

²log (x + 9) = ²log 2⁵

Nah, bentuk pada ruas kanan memang sengaja memindah 5 menjadi pangkat tanpa mengubah nilainya.

²log (x + 9) = ²log 2⁵

Karena angka basisnya sama, maka bisa langsung dicoret, hasilnya menjadi :

x + 9 = 32

x = 32 -9

x = 23

Jadi, nilai x pada persamaan ²log (x + 9) = 5 hasilnya 23.

Setelah itu, kamu uji numerusnya, (x + 9) = 23 + 9 = 32, karena 32 lebih dari nol, maka syarat sudah terpenuhi.

5. log (x² – 2x – 15) = log (x + 3), maka nilai x adalah …

Pada soal ini, pertama, selesaikan terlebih dahulu persamaannya menjadi :

x² – 2x – 15 = x + 3

x2 – 2x – 15 –x -3 = 0

x² – 3x – 18 = 0 (lalu difaktorkan)

(x – 6 ) (x + 3)

Jadi, x = 6 atau x = 3

Kemudian, kamu bisa mulai menguji syarat numerusnya.

Jika x = -3

f (x) = (-3)² – 2 (-3) – 15 = 0

Sedangkan g (x) = (-3)² + 3 = 12

Tidak memenuhi syarat.

Jika x = 6, maka hasilnya:

f(x) = 9 dan g(x) = 39

Maka, nilai x yang benar adalah 6.

Itulah pembahasan mengenai logaritma, syarat, dan contoh soalnya. Ternyata, matematika tidak se-menyeramkan itu, kan? So, pahami satu persatu dan perbanyak latihan soal agar menambah kemampuan. Selamat belajar!