Materi Bilangan Berpangkat – Pernahkan kamu mendengar istilah bilangan berpangkat? Atau bahkan belum pernah mendengarnya sama sekali?
Nah dalam kesempatan kali ini, kita akan bahas tuntas mengenai materi bilangan berpangkat, mulai dari pengertian bilangan berpangkat, jenis pembagian bilangan berpangkat, sifat-sifat bilangan berpangkat, dan operasi bilangan berpangkat beserta rumus dan contoh soal bilangan berpangkat.
Pengertian Bilangan Berpangkat
Apa itu bilangan berpangkat? Jadi, pengertian bilangan berpangkat adalah suatu bilangan yang digunakan untuk menyerdehanakan penulisan pada bilangan yang memiliki faktor-faktor pekalian sama atau perkalian berulang.
Coba deh bayangkan saja jika 9 kali 9 sebanyak 10 kali, bakal panjang banget tuh kamu menulisnya. 9x 9x 9x 9x 9x 9x 9x 9x 9x 9x. Itu baru sepuluh kali lho, kalo 30 kali atau 20 kali bahkan ratusan? Enggak kebayangkan jari kamu bakal keriting nulisnya hehe
Nah, dengan adanya bilangan berpangkat maka itu akan menjadi lebih sederhana yaitu 1010. Contoh lainnya yaitu:
- 4 x 4 x 4 x 4 x 4 x 4 perkalian tersebut bisa kamu ringkas dengan bilangan berpangkat menjadi 46.
- 6 x 6 x 6 x 6 x 6 dapat diringkas menjadi 65
Sedangkan untuk cara membacanya yaitu:
- 1010 dibaca sepuluh pangkat sepuluh
- 46 dibaca empat pangkat enam
- 65 dibaca enam pangkat lima
Pangkat yang tertera di atas berfungsi untuk menentukan jumlah faktor terulang.
Rumus bilangan berpangkat adalah:
an= axaxaxaxa… sebanyak n kali
Jenis Pembagian Bilangan Berpangkat
Adapun pembagian bilangan berpangkat dibagi menjadi beberapa jenis, diantaranya yang paling sering dibahas adalah bilangan berpangkat positif (+). Seperti yang dicontohkan sebelumnya, kemudian bilangan berpangkat negatif (-) dan bilangan berpangkat nol (0).
Supaya kamu lebih mudah memahami setiap jenis dari pembagian bilangan berpangkat, yuk ceki ceki ulasan di bawah ini!
1. Bilangan Berpangkat Positif (+)
Pengertian bilangan berpangkat positif adalah bilangan dengan eksponen pangkat positif. Apa sebenarnya eksponen? Eksponen yaitu nama lain dari pangkat. Untuk bilangan berpangkat positif itu sendiri memiliki beberapa sifat tertentu, dimana bilangannya terdiri atas a, b sebagai bilangan real dan m, n adalah bilangan bulat positif.
Adapun sifat-sifat khusus yang dimiliki oleh bilangan berpangkat positif adalah sebagai berikut:
amxan = am+n
am:an = am-n , berlaku untuk m>n serta b≠0
(am)n = amn
(ab)m = am bm
m = am/bm , dengan b≠0
Agar kamu lebih bisa memahami materi di atas, perhatikan dengan teliti contoh soal berikut ini ya.
Contoh soal bilangan berpangkat posistif dan jawabannya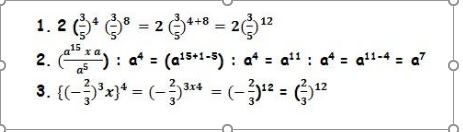
2. Bilangan Berpangkat Negatif
Pengertian bilangan berpangkat negatif adalah bilangan dengan eksponen pangkat negatif (-). Berbeda dengan bilangan berpangkat positif sebelumnya, bilangan berpangkat negatif memiliki sifat seperti:
Jika a∈R, a≠0 serta n adalah bilangan bulat negatif, maka:
a-n = 1/an atau 1/a-n = an
Agar kamu bisa lebih paham mengenai bilangan berpangkat negatif, yuk simak contoh soal berikut ini
Contoh soal bilangan berpangkat negatif dan jawabannya
1. Tentukan dan nyatakan dengan pangkat positif dari bilangan berpangkat berikut ini:
1/ 6(a + b)-7 = …. ?
Jawab:
1/ 6(a + b)-7 = = 1/6 (a+b)7
x1y2 / 2z6 = …. ?
Jawab:
x1y2 / 2z6 = 2-1x-1z-6 / y-2, dengan x ≠ 0 dan z ≠ 0.
3. Bilangan Berangkat Nol (0)
Tidak hanya bilangan berpangkat positif dan negatif, namun juga ada bilangan berpangkat nol lho. Lalu bagaimana menghitungnya ya? Kok 0? Nah daripada menerka-nerka, yuk simak materi bilangan berpangkat nol selengkapnya di bawah ini:
a0= 1 jika a adalah bilangan riil dan a≠0. Perhatikan contoh soal yang satu ini:
Contoh soal bilangan berpangkat nol dan jawabannyaSederhanakan bilangan 4(x3-y3)(x3-y3)0 !
Jawab:
4(x3-y3)(x3-y3)0 = 4(x3-y3)x1
= 4(x3-y3) dengan x3-y3 ≠0
Bagaimana, mudah kan?
Sifat-sifat Bilangan Berpangkat
Bukan hanya makhluk hidup saja yang memiliki sifat ya, bilangan berpangkat juga memiliki beberapa sifat. Semuanya mempunyai rumus penyelesaian masing-masing yang berbeda.
Apa saja sifat-sifat bilangan berpangkat?
- Pangkat bulat positif.
- Pangkat bulat negatif.
- Pangkat nol.
- Pangkat pecahan.
Simak penjelasan selengkapnya dari setiap sifat bilangan berpangkat dibawah ini.
1. Pangkat Bulat Positif
Pangkat bulat positif adalah bilangan pangkat yang paling umum kita jumpai. Seperti 23, dimana 2 adalah bilangan real dan pangkat 3 adalah bilangan positif. Sedangkan notasinya dapat dituliskan.
An = axaxa..xa
Dimana axaxa..x adalah n faktor.
Contoh:
42 = 4 x 4
= 16
53= 5 x 5 x 5
= 125
Sifat Pangkat Bulat Positif
Sifat pertama,
Jika a bilangan real, m dan n bilangan bulat positif sehingga amxan = am+n
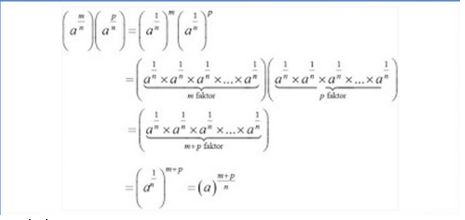
Pembuktian:
Sifat ini hanya berlaku jika a bilangan real dengan m dan n bilangan bulat positif. Jika m dan n bukan merupakan bilangan bulat positif, maka sifat pertama tersebut tidak berlaku ya.
Sifat kedua,
am/an= am-n berlaku bila a bilangan real dan a≠0, m serta n bilangan bulat positif.
Namun jika am dan an memiliki hasil 0, maka hasil bagi dari keduanya tidak menentu.
Sedangkan jika am= 0 serta an≠0 maka hasil baginya 0.
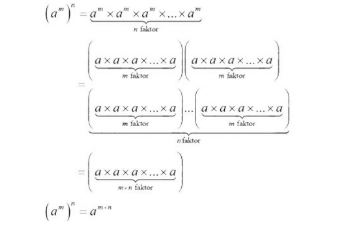
Sifat ketiga,
(am)n= amn
Pembuktian:
2. Pangkat Bulat Negatif
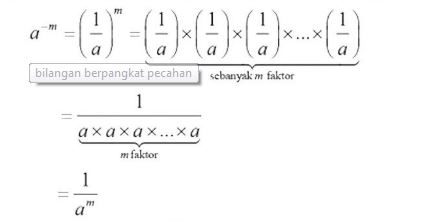
Yaitu bilangan berpangkat dengan a adalah bilangan real dan a≠0, m merupakan bilangan bulat positif, maka:
a-m = m
Nah dari uraian tersebut, maka dapat ditarik kesimpulan:
Agar kamu lebih mendalami materi tersebut, perhatikan contoh soal di bawah ini dengan seksama.
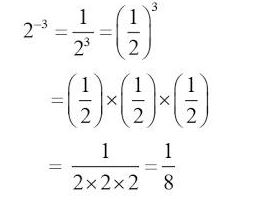
3. Pangkat Nol (0)
Merupakan bilangan berpangkat dengan a bilangan real serta a≠0, sehingga a0= 1.
Mengapa a tidak boleh 0? Hal ini dikarenakan, jika a=0 dan a0= 00 maka hasilnya akan menjadi tidak menentu.
Contoh:
50 = 1
70 = 1
4. Pangkat Pecahan
Merupakan pangkat dengan adanya pembilang dan penyebut, oleh sebab itu disebut pecahan. Contohnya a adalah bilangan real dengan a≠0, dan m adalah bilang bulat positif. Sehingga a1/m= p adalah bilangan real positif, jadi pm= a.
Beberapa Sifat Perpangkatan Bilangan Real
- am/n= (a1/n)m dengan a adalah bilangan real serta a≠0, m dan n bilangan bulat positif.
- (am/n)= a(p/n)= (a)m+p/n dengan a bilangan real serta a>0, p/n dan m/n adalah bilangan pecahan yaitu n≠0.
Pembuktian:

- (am/n)= (ap/q)= (a)m/n+p/q dengan a bilangan real a>0. Sehingga m/n serta p/q bilangan pecahan, q,n≠0.
Kesimpulan Sifat Bilangan Berpangkat
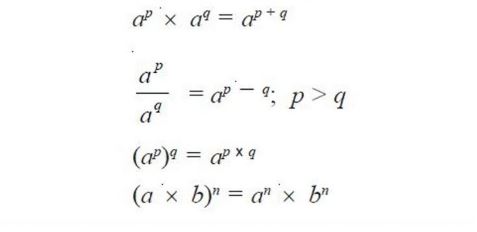
Sifat-sifat Operasi Bilangan Berpangkat
Adapun sifat-sifat operasi bilangan berpangkat dibagai menjadi 6 yaitu:
- Sifat Perkalian Bilangan Berpangkat
- Sifat Pembagian Bilangan Berpangkat
- Sifat Perpangkatan Bilangan Berpangkat
- Sifat Perpangkatan Perkalian Dua Bilangan
- Sifat Perpangkatan Pembagian Dua Bilangan
- Sifat Perpangkatan Bilangan 0 (Nol)
Nah setelah kita mengetahui sifat-sifat operasi bilangan berpangkat, sekarang kita akan lanjut bahas satu per satu mengenai sifat operasi bilangan berpangkat lengkap dengan contoh soal operasi bilangan berpangkat. Yuk simak pembahasannya di bawah ini.
1. Sifat Perkalian Bilangan Berpangkat
Adapun Rumus Perkalian Bilangan Berpangkat adalah
Uraian:
24x22 = (2x2x2x2) x (2×2)
24x22 = 2x2x2x2x2x2
24x22 = 26
2. Sifat Pembagian Bilangan Berpangkat
Adapun Rumus Pembagian Bilangan Berpangkat adalah
uraian:
24:22 = (2x2x2x2) : (2×2)
24:22 = (2×2)((2×2)x(2×2))
24:22 = 22
3. Sifat Perpangkatan Bilangan Berpangkat
Adapun Rumus Perpangkatan Bilangan Berpangkat adalah
Uraian:
(34)2 = (3x3x3x3)2
(34)2 = (3x3x3x3) x (3×3)
(34)2 = 36
4. Sifat Perpangkatan Perkalian Dua Bilangan
Adapun Rumus Perpangkatan Perkalian Dua Bilangan adalah
Uraian:
(2×3)2 = (2×3) x (2×3)
(2×3)2 = (2×2) x (3×3)
(2×3)2 =22 x 32
5. Sifat Perpangkatan Pembagian Dua Bilangan
Adapun Rumus Perpangkatan Pembagian Dua Bilangan adalah
Uraian:
(4:3)2 = (4:3) x (4:3)
(4:3)2 = (4×4) : (3×3)
(4:3)2 = 42:32
6. Sifat Perpangkatan Bilangan 0 (Nol)
Adapun Rumus Perpangkatan Bilangan 0 (Nol) adalah
a0 = 1
0n = 0
00= tidak terdifinisi
Uraian:
a0 = 1
32 : 32 = 32 -32 = 30 sehingga,
32 : 32 = 30 karena 32 : 32 = 9 : 9 = 1 maka
30 = 1
0n = 0
03 = 0x0x0 = 0
00 = tidak terdefinisi, yaitu dapat melibatkan semua bilangan, entah itu 1, 12, 123 atau 1234 dan seterusnya.
Jadi itulah ulasan mengenai bilangan berpangkat, mulai dari pengertian bilangan berpangkat, jenis pembagian bilangan berpangkat, sifat-sifat bilangan berpangkat, dan operasi bilangan berpangkat beserta rumus dan contoh soal bilangan berpangkat.
Dengan adanya perpangkatan semua perkalian dengan bilangan yang sama dan memiliki faktor dapat dirangkum menjadi lebih ringkas dan lebih mudah untuk dipecahkan masalahnya. Akhirnya pembelajaran kali ini mengenai bilangan berpangkat telah selesai, Jangan lupa terus semangat belajar ya!

