Persamaan Garis Lurus

Persamaan garis lurus adalah pernyataan yang mengartikan jika suatu garis lurus masuk dalam suatu persamaan. Karateristik dari persamaan garis lurus yakni memiliki variabel dengan kuadrat tertinggi satu.

Garis lurus sendiri adalah sekumpulan titik-titik dengan jumlah tidak terhingga dan saling berdampingan. Suatu garis lurus, umumnya bisa dinyatakan dalam satu persamaan atau lebih. Berikut contoh pernyataan persamaan garis lurus:

• y = mx
• y = -mx
• ax + by = ab

Dari contoh persamaan garis lurus di atas, m adalah gradien, sementara x adalah variabel dan c adalah konstanta.

Pengertian Persamaan Garis Lurus

Pengertian persamaan garis lurus adalah jika kita gambarkan dalam suatu bidang koordinat Cartesius, maka akan terbentuk suatu garis lurus. Nah yang dimaksud garis lurus sendiri adalah kumpulan titik-titik dengan letak sejajar.

Dimana persamaan ini bisa berbentuk garis yang saling tegak lurus atau sejajar.

Gradien

Dalam sistem persamaan ini, Anda juga akan sangat familiar dengan gradien. Gradien yakni suatu perbandingan komponen x dan komponen y, atau biasa disebut kecondongan suatu garis. Simbol gradien ialah huruf “m”.

Cara Menemukan Gradien pada Persamaan Garis Lurus

Dalam suatu garis lurus, Anda bisa menentukan gradien dengan cara berikut:

1. Gradien dari garis lurus ax + by + c = 0

Maka M = komponen x / komponen y

2. Gradien yang melewati titik pusat (0,0) dengan titik (a,b)

Maka m = b/a

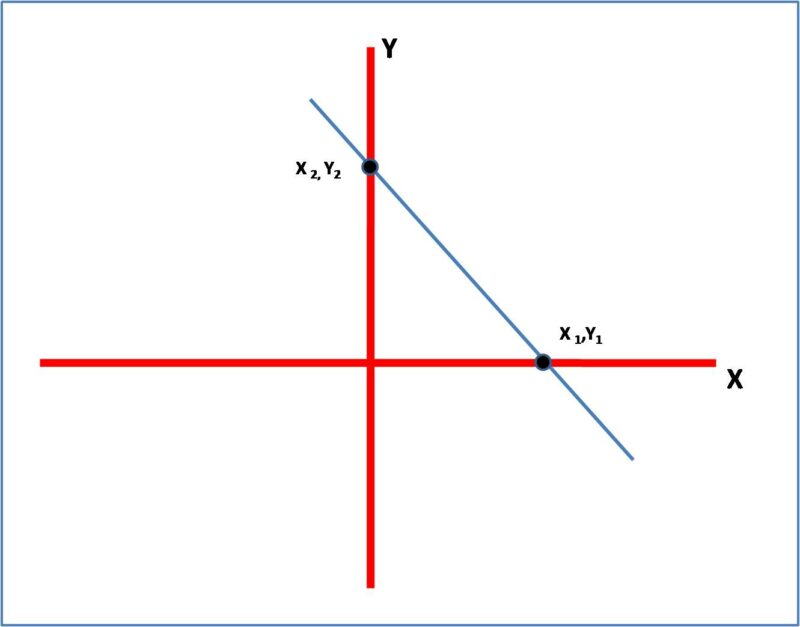
3. Gradien yang melewati titik ( x₁, y₁) dan ( x₂, y₂ )

Maka m =  y₂ – y₁ / x₂ – x₁ atau y₁ – y₂ / x₁ – x₂

4. Gradien garis yang sejajar (/ /)

Maka m = sama atau jika disimbolkan dalam bentuk m₁ = m₂

5. Gradien garis tegak lurus (kebalikan dan lawan)

Maka m = -1 atau  m₁ x m₂ = -1

Posisi Antara 2 Garis

Dalam sistem persamaan garis lurus, posisi antara 2 garis bisa dibedakan menjadi 2 yakni, sejajar dan tegak lurus. Kedua posisi ini memiliki persamaan garis lurus yang berkaitan satu sama lain. Dengan begitu, jika ada 1 persamaan garis yang sudah diketahui, maka garis yang sejajar/tegak lurus dengan garis tersebut dapat diketahui.

1. Garis yang Sejajar

Garis sejajar adalah dua garis yang tidak memiliki titik potong, gradien pada kedua garis pun sama. Contohnya, gradien pada garis g = m_g dan gradien dari garis h = m_h. Jadi, hubungan dari gradien 2persamaan garis tersebut bisa dinyatakan dalam kalimat: m_g   = m_h.

2. Garis yang Tegak Lurus

Hubungan dari dua garis tegak lurus bisa dinyatakan jika gradien keduanya saling berlawanan atau kebalikan. Atau dengan kata lain, garis tegak lurus merupakan garis yang jika dikalikan 2 buah gradien, maka hasilnya sama dengan -1.

Contohnya, gradien garis pertama adalah m₁ = 2 berarti gradien garis kedua adalah m₂ = -1/2.

Rumus Persamaan Garis Lurus

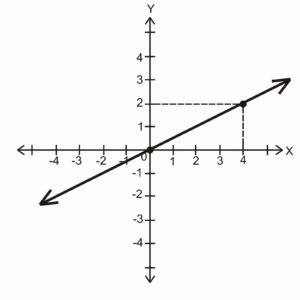
Dalam pelajaran SMP, biasanya ada dua tipe soal persamaan garis lurus. Pertama, tipe yang mana gradien dan satu titik potong sudah diketahui. Tipe kedua yakni persamaan yang sudah diketahui dua titik potongnya.

Masing-masing tipe tersebut bisa diselesaikan dengan rumus berikut:

1. Persamaan garis dengan gradien m serta melewati titik A(x₁.y₁), maka rumusnya:

y – y₁ = m(x – x₁)

2. Persamaan garis yang melewati titik A(x₁.y₁) dan B(x₂.y₂), maka rumusnya:

y – y₁ / y₂ . y₁ = y – x₁ / x₂ . x₁

Contoh Persamaan Garis Lurus

1. Pertama pelajari persamaan Garis Lurus dengan Bentuk Umum ( y = mx). Persamaan yang melewati titik pusat (0,0) dan gradiennya m.

Contoh Soal:

Tentukan persamaan garis lurus yang melewati titik pusat (0,0) dan gradiennya 2.

Jawab:

y = mx

y = 2x

2. Persamaan garis lurus yang melewati titikm sejajar (y = mx + c)

Persamaan garis lurus yang sejajar dengan y = mx dan gradiennya m.

Persamaan garis yang melewati titik (0,c) dan gradiennya m. (0,c) merupakan titik potong sumbu y.

3. Persamaan garis lurus yang melewati titik (x₁ , y₁) serta gradiennya m.

Bentuk persamaanya adalah: y – y₁ = m ( x – x₁ )

4. Persamaan garis lurus dengan yang melewati 2 titik yakni (x₁ , y₁) serta (x₂ , y₂).

Bentuk persamaanya adalah: y – y₁ / y₂ – y₁ = x – x₁ / x₂ – x₁

Contoh Soal Persamaan Garis Lurus dan Pembahasannya

Soal 1.

Cari persamaan garis lurus yang melalui titik potong garis dengan persamaan 3x + 2y – 12 serta 5x + 2y = 16 dan sejajar dengan 2x + 7 = 4.

Jawab:

3x + 2y = 12

5x + 2y = 16-

– 2x = -4
x = -4 / -2 = 2

 

3x + 2y  = 12

3 x 2 + 2y = 12

6 + 2y = 12

2y = 6

y = 6 / 2 = 3

Titik potong (2,3) sejajar 2x + y = 4, maka

m₁ = -a / b = -2 / 1 = -2

m₁ = m₂ = -2

y – y₁ = m₂ (x – x₁)

y – 3 = -2 (x – 2)

y – 3 = -2x + 4

2x + y – 3 + 4 = 0

2x + y + 1 = 0

Soal 2.

Persamaan garis yang melewati (-1,2) dan tegak lurus dengan garis 4y = -3x + 5 ialah…

1. 3x + y + 5 = 0
2. 3x + 4y + 5 = 0
3. 4x – 3y + 10 = 0
4. 4x – 3y – 10 = 0

Jawab:

Cari gradien garis 4y = -3x + 5

4y= -3x + 5

y = -3/4x + 5/4

Jadi gradien dari garis tersebut adalah m = -3/4

Suatu garis bisa tegak lurus dengan persamaan garis jika memiliki gradien yang memenuhi:

m₁ x m₂ = -1

-3/4 x m₂ = – 1

m₂ = – 1 / -3/4

m₂ = 4/3

Selanjutnya, cari persamaan garis dengan menggunakan gradien m₂ = 3/4 yang melalui titik (-1, 2)

y – y₁ = m₂ (x – x₁)

y – 2 = 4/3 (x – (-1))

y – 2 = 4/3 (x + 1)

3(y – 2) = 4 (x + 1)

3y – 6 = 4x + 4

– 4x + 3y – 10 = 0

4x – 3y + 10 = 0

Jadi, jawaban yang tepat adalah C.

Umumnya, soal yang muncul dalam ujian adalah bentuk soal cerita seperti contoh nomor 2. Jadi untuk mempersiapkan ujian, Anda bisa mempelajari contoh-contoh soal serupa.