Pengertian Vektor matematika adalah suatu besaran dengan arah, vektor tersebut digambarkan dengan panah yang arahnya menunjukkan ke arah vektor dan panjang garisnya merupakan besar vektor. Jika sebuah vektor dimulai dari titik A ke titik B, jadi vektor tersebut ditulis menggunakan huruf kecil dan bagian atasnya diberi tanda garis atau panah 
. Selain itu, juga dapat ditulis seperti ilustrasi berikut ini:
Contohnya, vektor 
merupakan vektor yang bermula di titik A(x1.x1) ke titik B (x2.x2) sehingga dapat dituangka dalam koordinat cartesius di bawah.
Panjang garis sejajar pada sumbu x adalah v1= x2 – x1 dan panjang garis sejajar y merupakan v2= y2 – y1 yang merupakan komponen vektor .
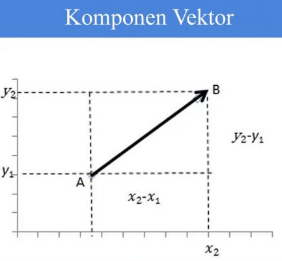
Selain dinyatakan dalam koordinat cartecius, vektor juga dapat dinyatakan dalam aljabar, yaitu :
Jenis-Jenis Vektor
Vektor memliki beberapa jenis yang berbeda, yaitu antara lain:
1. Vektor Posisi
Vektor posisi merupakan vektor yang memiliki titik awal di 0 (0,0) serta berakhir pada titik A (a1,a2).
2. Vektor Satuan
Vektor satuan adalah sebuah vektor yang mempunyai panjang satu – satuan. Vektor satuan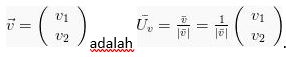 
3. Vektor Nol
Vektor nol merupakan vektor yang memiliki panjang tidak jelas, karena panjangnya nol dan dinotasikan dengan 
.
4. Vektor Basis
Vetor basis adalah vektor satuan tegak lurus, dimana dalam vektor ruang R2 atau dua dimensi terdapat 2 vektor basis yaitu 
serta 
. Sedangkan dalam vektor 3 dimensi atau R3 memiliki vektor basis yaitu 
serta 
.
Macam – Macam Sekaligus Operasi Vektor
Selain memiliki beberapa jenis, vektor matematika ternyata juga terdiri atas beberapa macam. Ingin tau apa saja macam dari vektor? Nah berikut ini macam-macam vektor matematika besera operasinya, perhatikan dengan seksama ya.
Vektor pada R2
Panjang pada suatu segmen garis yang menyatakan vektor dinotasikan dengan lambang ataupun dapat juga dilambangkan dengan notasi | |. Di bawah ini panjang dari sebuah vektor dapat kamu lihat seperti berikut ini:
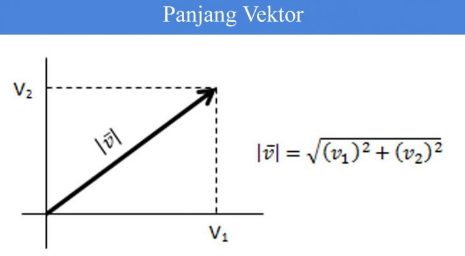
Sedangkan panjang vektor merupakan bentuk yang bisa dikaitkan melewati sudut ∅ sehingga dapat dibentuk oleh vektor serta sumbu positif dengan mudah.
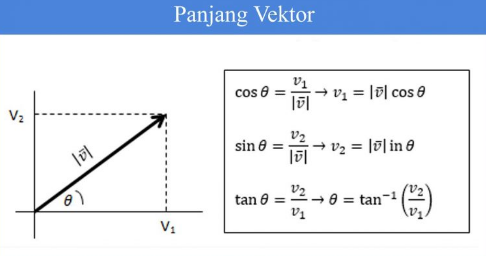
Operasi Vektor pada R2
Proses penjumlahan serta pengurangan vektor pada R2.
Resultan merupakan sebutan untuk hasil dari penjumlahan pada 2 vektor atau lebih.
Penjumlahan pada vektor tersebut juga bisa dilakukan dnegan aljabar dan dapat juga dilakukan memakai cara penjumlahan komponen yang berposisi sama atau seletak.
Jika :
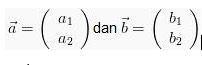
Maka:
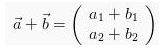
Sehingga penjumlahan vektor secara grafis dapat dilihat pada contoh ilustrasi seperti di bawah ini:
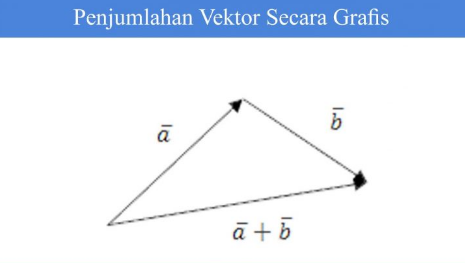
Hal ini juga berlaku pada pengurangan vektor, jadi apa yang terjadi pada penjumlahan vektor juga diberlakukan hal yang sama pada pengurangan vektor. Dapat dilihat seperti di bawah ini:
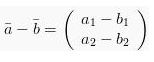
Sedangkan sifat-sifat yang dimiliki oleh penjumlahan vektor yaitu:
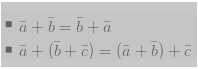
- Perkalian Vektor R2 dengan Skalar
Sebuah vektor dapat juga dilakukan dengan belangan real atau suatu skalar dimana selanjutnya akan menghasilkan suatu vektor yang baru bilamana merupakan vektor serta k adalah skalar.
Sehingga perkalian vektor dapat ditulis ke dalam bentuk seperti di bawah ini:
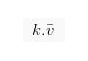
Di bawah ini adalah keterangan selengkapnya:
Jika k > 0, maka vektor 
menjadi searah dengan vektor .
Jika k < 0, maka vektor menjadi berlawanan dengan arah vektor .
Jika k = 0, maka vektor adalah vektor identitas yakni 
.
Apabila secara grafis perkalian tersebut bisa mengubah panjang vektor dan bisa dilihat pada tabel di bawah ini:
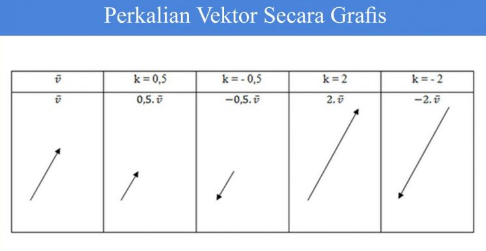
Sedangkan jika dengan aljabar, perkalian pada vektor terhadap skalar k bisa dirumuskan seperti berikut ini:
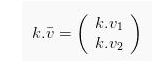
- Perkalian Skalar Dua pada Vektor R2
Pada perkalian skalar dua vektor dapat sebagai hasil kali antara titik dua vektor yang kemudian bisa dituliskan seperti di bawah ini:
Vektor pada R3
Vektor yang terdapat pada ruang 3 dimensi atau R3 (x,y,z) yang mana jarak antara 2 titik vektor dalam ruang tiga dimensi dapat diketahui dengan rumus phytagoras.
Jika bermula dari titik A (x2,y2,z2) dan B (x2.y2.z2) yaitu:
Atau jika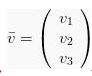 
, maka:
Vektor 
dapat dinyatakan ke dalam dua bentuk, yaitu dinyatakan dalam kolom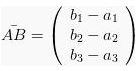 
atau dinyatakan dalam baris 
.
Selain itu, vektor juga dapat dinyatakan sebagai kombinasi linier dari vektor basis 
atau 
ataupun 
, berikut ini ilustrasi selengkapnya:
Operasi Vektor pada R3
Operasi vektor yang terjadi pada R3, pada umumnya memilliki landasan yang sama dengan operasi vektor pada R2, seperti dalam pengurangan, penjumlahan hingga perkalian. Agar kamu lebih memahami, simak materinya di bawah ini ya.
- Penjumlahan dan Pengurangan Vektor pada R3
Penjumlahan serta pengurangan vektor pada R3, sama dengan penjumlahan dan pengurangan pada R2, yaitu:
- Perkalian Vektor pada R3dengan Skalar
Jika adalah vektor serta k adalah skalar, sehingga perkalian vektor menjadi:
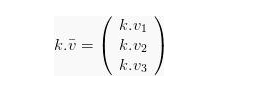
- Hasil Kali dari Skalar Dua Vektor
Selain rumus yang terdapat pada R3 ada juga rumus dalam hasil skalar dua vektor. Jika 
merupakan:
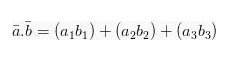
Proyeksi Orthogonal Vektor
Jika vektor ā diproyeksikan, kemudian menjadi vektor barb dan dinotasikan dengan 
, seperti yang terlihat pada gambar di bawah ini:
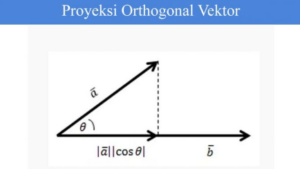
Diketahui:
Maka:
Untuk mendapatkan vektornya:
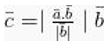
Notasi Vektor
Seperti yang sudah disinggung di atas, vektor dituliskan dengan huruf yang selanjutnya pada bagian atas dikasih arah garis. Vektor dapat dinyatakan ke dalam dua dimensi, tiga dimensi atau bahkan lebih dari itu.
Jika suatu vektor dinyatakan dalam R3 maka vektor satuannya dinyatakan dengan i j serta k.
i = vektor absis (searah sumbu x)
j = vektorr ordinat ( searah sumbu y)
k = vektor aplikat (searah sumbu z)
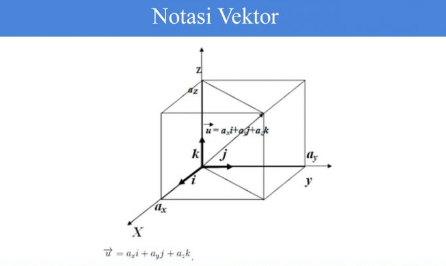
Dimana a_x komponen sumbu x, a_y komponen sumbu y serta a_z adalah komponen arah sumbu z.
Vektor tersebut dituliskan:
Pada ilmu matematika lebih umum ditulis:
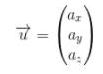
selanjutnya dalam bentuk indeks angka:
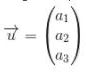
Besar serta nilai vektor dituliskan layaknya tanda mutlak pada aljabar yaitu:
atau bisa dituliskan dalam indeks angka menjadi
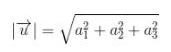
apabila vektor yang ada ditentukan oleh koordinat maka:
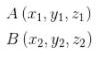
sehingga vektor AB dinyatakan dalam
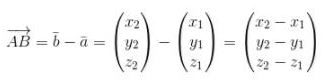
selanjutnya panjang vektor AB
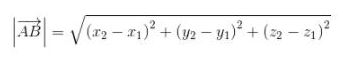
sedangkan vektor satuan dari vektor tertentu dinyatakan sebagai:
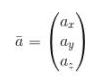
Dinyatakan dengan:
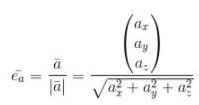
Contoh Soal Vektor Matematika:
Diketahui vektor pada titik A, B dan C seperti pada gambar di bawah ini, maka tentukan persamaan vektor C!
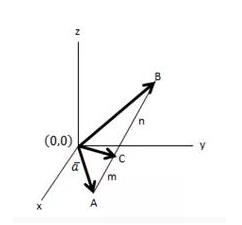
Penyelesaian:
Dari gambar di atas maka dapat kita ketahui hal-hal sebagai berikut:
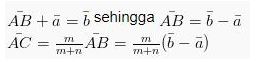
Sehingga:
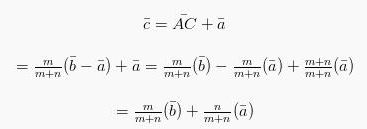
Bagaimana, mudah kan? Jika belum begitu memahaminya, kamu dapat membaca ulang materi yang ada ya.
Nah, itu dia ulasan mengenai vektor matematika lengkap dengan ilustrasi, semoga materi pembahasan di atas dapat kamu jadikan bahan belajar yang menyenangkan ya.
