Pada materi dasar matematika, mungkin kamu akan banyak belajar tentang penjumlahan, pengurangan, perkalian, pembagian ataupun teori geometri dasar.
Namun tahukan kamu, jika perasi dasar layaknya perkalian dan penjumlahan dasar memang begitu erat kaitannya dengan matriks. Tapi hal tersebut secara langsung tidak selalu diterapkan, karena matriks jauh lebih rumit dibandingkan dengan angka.
Materi operasi yang terdapat pada matriks sendiri meliputi operasi hitung pengurangan, penjumlahan dan perkalian matriks. Tentunya, operasi hitung inilah yang nantinya bisa dilakukan apabila dua buah matriks mempunyai ukuran yang sama.
Sedangkan pada perkalian matriks sendiri, operasi hitung bisa dilakukan jika pada matriks pertama tersebut mempunyai kolom yang jumlahnya sama banyak dengan jumlah baris pada matriks yang kedua.
Di dalam ulasan ini nantinya kamu akan berusaha mempelajari tentang bagaimanakah cara melakukan operasi hitung antar elemen yang ada di dalam sebuah matriks, dan bagaimana cara melakukan matriks dasar dan operasi matriks itu sendiri, berupa pengurangan dan penjumlahan yang begitu sederhana.
Dalam materi matriks dasar, kamu bisa mengetahui jenis – jenis matriks, yakni:
- Matriks baris: matriks yang hanya memiliki satu baris.
- Matriks nol: matriks yang semua elemennya adalah nol.
- Matriks kolom: matriks yang hanya memiliki satu kolom.
- Matriks persegi: matrik yang memiliki jumlah baris serta kolom sama.
- Matriks identitas: matriks konstanta yang memiliki elemen diagonal utama 1.
Penjumlahan pada Matriks
Apabila diketahui terdapat dua matriks yang kemudian memiliki kolom dan juga baris yang sama, maka tentunya kamu dapat membentuk keduanya untuk bisa memperoleh nilai matriks baru dengan ordo yang sama juga.
Jadi salah satu daripada syarat untuk dapat menjumlahkan dua matriks atau lebih, yaitu harus memiliki ordo yang sama. Sebagai permisalan adalah matriks A dan B yang memiliki ordo m x n atau biasanya ditulis dengan A = [aij] m×n , B = [bij] m×n Dengan i = {1,2,…,m} dan j = \{1,2,\dots,n\} j = {1,2,…,n}.
Kemudian akan bertemu pada persamaan C = [cij] m×n, dimana C = A + B
C = A + B dengan c_{ij} = a_{ij} + b_{ij} cij = aij + bij
Sebagai contoh saja
Misalnya ada matriks A dan B yang mana diartikan sebagai berikut:
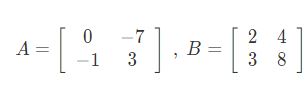
Maka untuk mencari matriks C maka diperlukan disini adalah penjumlahan antara matriks A dan B Sehingga nantinya akan diperoleh:
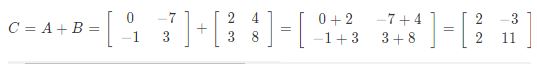
Di samping pada matriks dasar dan operasi matriks, kamu juga dapat mempergunakan operasi pengurangan dengan syarat, harus memiliki ordo yang sama sebagai contoh ketika kamu ingin menghitung:
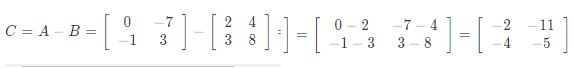
Kemudian bagaimana jika memang terdapat dua matriks yang memiliki ordo berbeda yang mana, keduanya dapat dijumlahkan atau tidak, sebagai permasalahan saja apabila terdapat matriks D dengan ordo 2 * 3 dan apabila ditanya a + d maka a + d = tidak memiliki definisinya dikarenakan ordo a tidak sama dengan ordo d.
Adanya Perkalian dengan Skalar
Sebagai permisalan saja apabila ada matriks dasar dan operasi matriks A = [aij] m×n dan a merupakan sembarangan skalar atau yang biasa dengan kompleks atau Ridho maka Perkalian antara matriks dengan skalar a tersebut bisa dibentuk dengan mengalihkan setiap elemen.
a_{ij} aij dengan aij α, sebagai contoh adalah jikalau a = 2, β = 1 + 2i Matriks a didefinisikan sebagai berikut:
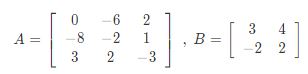
Kemudian cobalah untuk menentukan hasil dari aA dan bB
Penyelesaiannya maka Kamu bisa menyelesaikan dengan cara mengalikan skalar dengan setiap elemen yang terdapat pada matriks A Sehingga nantinya aA akan diperoleh seperti berikut ini:
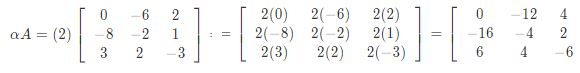
dengan cara yang sama maka Kamu juga bisa

Perkalian Dua Matriks
Kemudian pada matriks dasar dan operasi matriks sendiri yang pertama harus kamu pelajari adalah, perkalian antara vektor dengan pada kolom dan juga barisnya. Lalu apa yang dimaksud vektor kolom dan baris?
Vektor kolom sendiri merupakan matriks yang mempunyai ordo N * 1 dengan elemen sebanyak n contoh adalah sebagai berikut:
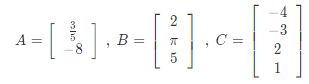
Faktor baru sendiri merupakan matriks yang mempunyai ordo 1 * n dengan elemen sebanyak 2 contoh.
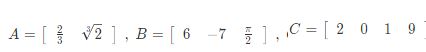
Perkalian Yang Terdapat Pada Kolom Dan Baris
Kemudian salah satunya terdapat perkalian antara vektor kolom dan baris sebagai permisalan saja adalah
A = [a_{i}]_{1 \times n}
A = [ai]1×n dan B = [b_{i}]_{n \times 1}
B = [bi] n×1
Yang mana berturut – turut adalah vektor baris dan kolom dengan n elemen dan i = {1,2,….,n}. apabila kedua motor tersebut dikalikan maka akan diperoleh:
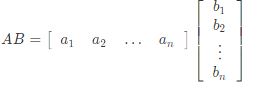
![]()
Keunikan yang berasal dari perkalian antara vektor baris dan kolom ini berupa bilangan bukan matriks.
Perkalian Antara Matriks Secara Umum
Apabila telah berhasil mempelajari perkalian antara vektor kolom dan 3 baris maka selanjutnya, kamu harus mempelajari terlebih dahulu perkalian antara dua matriks sembarang dengan ukuran beserta dengan ketentuannya.
Sebagai permasalahan sosial apabila terdapat dua matriks yaitu A = [aij]l×m dan B = [b_{ij}]_{m \times n} B = [bij]m×n, Selain itu juga terdapat matriks C dengan c = ab maka bisa dituliskan dalam setiap elemen dari C tersebut sebagai berikut:
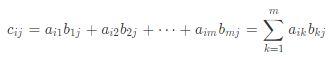
ci = ai1b1j + ai2b2j + ⋯ + aimbmj = k = 1∑maikbkj. Apabila hal ini ada kaitannya dengan vektor kolom dan baris maka kemudian dapat didefinisikan sebagai ai dan bj, dimana berturut – turut adalah vektor baris ke – i dan matriks A serta vektor kolom ke – 3 dari matriks B. Kemudian elemen dari C tersebut bisa juga ditulis cij = aibj.
Jika didasarkan pada pernyataan yang ada, maka bisa ditarik kesimpulan atau perkalian dua matriks AB sendiri bisa terjadi apabila banyak kolom a sama dengan banyak baris B.
Trace Matriks
Trace matriks yang asalnya dari matriks persegi ialah hasil penjumlahan dari elemen – elemen pada diagonal utama matriks. Jadi sebagai syarat untuk dapat mencari matriks yaitu matriksnya sendiri sehingga memiliki ordo n x n. Sehingga penulisannya dapat disimbolkan dengan t kanrace A) = tr(A)
Sifat-Sifat Dari Pada Operasi Matriks
Sebagai catatan, pembahasan sifat – sifat operasi ini memang bisa dilakukan dengan cara mengangkat wawasan ukuran matriks tersebut. Serta dapat dioperasikan menyesuaikan dengan ketentuan yang berasal dari setiap operasi itu sendiri.
Terhadap operasi penjumlahan
Sebagai permisalan saja jika terdapat matriks ABC dan matriks nol O makan nantinya akan muncul sebuah persamaan seperti dibawah ini
- A + B = B + A
- A + (B + C) = (A + B) + C
- A + (B + C) = (A + B) + C
- A + O = O + A = A
- A + O = O + A = A
- A + ( -A) = -A + A = O
- A + (−A) = −A + A = O
Terhadap Operasi Perkalian
Sebagai permisalan jika terdapat matriks A, B, C dimana matrik nol O, matriks yang memiliki identitas I dan m, n sembarangan bilangan bulat sendiri maka nantinya akan berlaku juga.

Matriks Terhadap Penjumlahan Dan Juga Perkalian Dengan Skalar
Sebagai permisalan saja apabila terdapat matriks A, B, C dan m, n, maka nantinya akan berlaku:
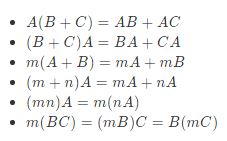
Terhadap Operasi Transpose
Apabila terdapat matriks A,B dan a sembarang scalar, yang demikian nantinya akan berlaku juga:
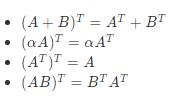
Berkaitan Dengan Operasi Trace
Sebagai contoh, apabila terdapat matriks A, B, I dimana ini adalah identitas dan a sembarang skalar serta sembarangan bilangan bulat n yang sedemikian rupa sehingga nantinya akan berlaku:
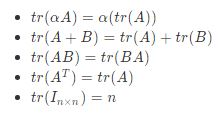
Contoh Soal Matriks Dasar
Terdapat sebuah perkalian matriks![]() menghasilkan matrik nol. Carilah nilai x yang memenuhi persamaan di atas.
menghasilkan matrik nol. Carilah nilai x yang memenuhi persamaan di atas.
Jawab:

Jadi, nilai x yang memenuhi persamaan di atas adalah x1 = 2 dan x2 = 3.
Tidak sulit bukan mengenal matrik dasar? Kamu bisa belajar lebih banyak dengan mengerjakan contoh – contoh soal tentang matriks.

