Irisan Kerucut – Kalau kamu sudah pernah mendapatkan materi tentang bangun ruang, pastinya sudah mengenal apa itu kerucut. Ya, betul sekali, kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran. Sedangkan jumlah sisinya ada dua, yakni alas lingkaran dan sisi lengkung sebagai selimutnya. Nah, pada materi kali ini, akan dibahas tentang irisan kerucut.
Perlu kamu ketahui bahwa apabila kerucut diiris dari arah yang berbeda, maka akan menghasilkan beberapa bangun. Beberapa hasil dari irisan kerucut seperti elips, lingkaran, parabola, serta hiperbola.
Coba kamu perhatikan gambar berikut ini!
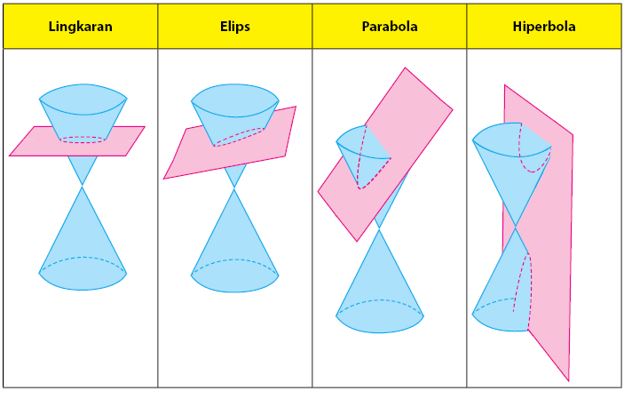
Dari gambar itu, kamu jadi tahu apa saja hasil irisan kerucut!
- Apabila kerucut dipotong mendatar, maka potongannya akan berbentuk lingkaran.
- Apabila dipotong menggunakan arah sudut tertentu, maka terbentuk lah elips ataupun parabola.
- Apabila dipotong dengan arah tega, maka bangun ruang yang dihasilkan adalah hiperbola.
Setelah kamu tahu apa saja hasil irisan kerucut, yuk, kita uraikan satu per satu!
1. Irisan Kerucut Lingkaran
Irisan kerucut yang pertama adalah lingkaran. Seperti yang sudah dibahas, lingkaran dihasilkan saat kerucut dipotong mendatar. Bentuk umum dari persamaan lingkaran sendiri dibedakan jadi dua. Perbedaan ini didasarkan pada pusat lingkaran itu sendiri.
Pusat lingkaran yang pertama ada pada tengah koordinat kartesius atau O (0, 0). Ada juga yang berlokasi di koordinat kartesius tertentu atau di titik P (a, b). Bentuk persamaan lingkaran juga diberikan pada bentuk yang lain, yakni x2 + y2 + Ax + By + C = 0.
- Persamaan lingkaran Pusat O (0, 0), jari-jari r adalah x2 + y2 = r2
- Persamaan lingkaran pada pusat P (a, b) dengan jari-jari r adalah (x – a)2 + (y – b)2 = r2
- Bentuk umum persamaan lingkaran yang bisa dipakai untuk kedua bentuk tersebut adalah x2 + y2 + Ax + By + C = 0, dengan pusat = (-1/2 A, -1/2 B), sedangkan jari-jari atau r = √1/4 A2 + 1/4 B2 – C
Selanjutnya, ada elips, yuk, bahas bareng!
2. Irisan Kerucut Elips
Hasil irisan kerucut yang satu ini berbentuk laiknya lingkaran yang dipipihkan. Ada beberapa bagian elips yang harus kamu ketahui, yakni sumbu minor, sumbu mayor, puncak elips, fokus elips, loctus rectum, serta pusat elips. Jenis dari elips ada dua, yaitu elips vertikal dan elips horizontal.
Kamu bisa lihat perbedaan gambar elips horizontal dan vertikal di bawah ini!
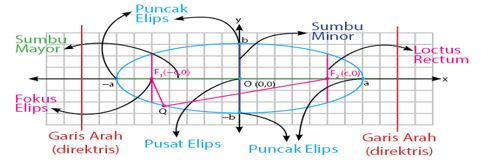
Elips Horizontal
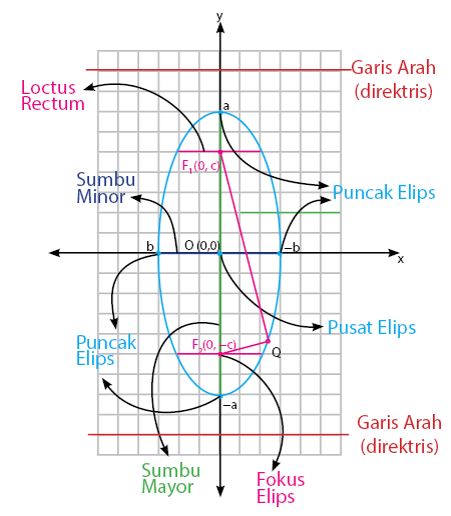
Elips Vertikal
Persamaan Elips Horizontal
Pada elips horizontal, terbagi lagi menjadi dua jenis, diantaranya:
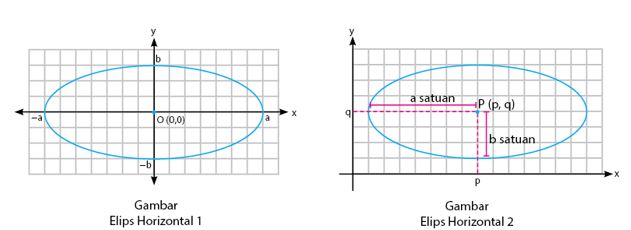
Dari dua jenis elips horizontal tersebut, maka bisa diperoleh persamaan berikut:
| Keterangan | Bentuk Elips Horizontal 1 | Bentuk Elips Horizontal 2 |
| Pusat | O (0, 0) | P (p, q) |
| Fokus | (+ c, 0) | (p + c, q) |
| Panjang Sumbu Mayor | 2a | 2a |
| Panjang sumbu minor | 2b | 2b |
| Puncak | (+a, 0) dan (0, +b) | (p + a, q) dan (p, q + b) |
| Bentuk umum persamaan | x2/a2 + x2/b2 = 1 | (x – p)2/a2 + (y – q)2/b2 = 1 |
| Gari arah atau direktris | X = + a2/c | X = p + a2/c |
| Panjang Loctus Rectum | LR = |2b2/a| | LR = |2b2/a| |
| Eksentrisitas | e = c/a | e = c/a |
Persamaan Elips Vertikal
Bentuk irisan kerucut berupa elips vertikal juga terbagi menjadi dua, silakan kamu lihat gambar berikut ini!
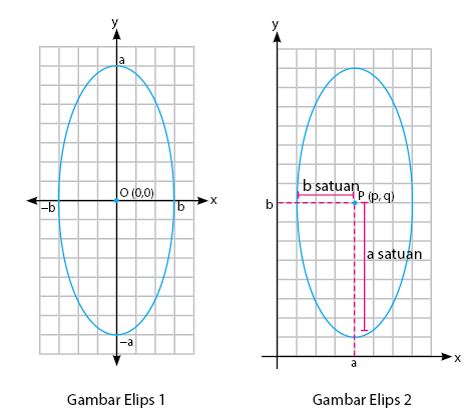
Dari gambar tersebut, maka akan didapatkan beberapa persamaan, yakni :
| Keterangan | Bentuk Elips Horizontal 1 | Bentuk Elips Horizontal 2 |
| Pusat | O (0, 0) | P (p, q) |
| Fokus | (+ c, 0) | (p + c, q) |
| Panjang Sumbu Mayor | 2a | 2a |
| Panjang sumbu minor | 2b | 2b |
| Puncak | (+a, 0) dan (0, +b) | (p + a, q) dan (p, q + b) |
| Bentuk umum persamaan | x2/a2 + x2/b2 = 1 | (x – p)2/a2 + (y – q)2/b2 = 1 |
| Gari arah atau direktris | X = + a2/c | X = p + a2/c |
| Panjang Loctus Rectum | LR = |2b2/a| | LR = |2b2/a| |
| Eksentrisitas | e = c/a | e = c/a |
Hubungan antara fokus dan puncak pada elips akan memenuhi persamaan berikut :
- Apabila a > b pada elips horizontal, maka persamaannya menjadi a2 = b2 + c2
- Apabila a < b pada elips vertikal, maka persamaannya jadi b2 = a2 + c2
Pembahasan tentang elips sudah selesai, kita lanjut ke irisan kerucut yang selanjutnya, yakni parabola. Yuk, simak bersama!
3. Irisan Kerucut Parabola
Parabola memiliki bentuk seperti kurva mulus yang ada pada persamaan kuadrat. Nah, materi yang akan kamu terima pada pembahasan ini adalah parabola dengan bentuk yang terbuka ke atas dan ke bawah. Parabola juga bisa dibedakan berdasarkan titip puncaknya. Ada yang bersumbu O (0, 0), atau bersumbu P (a, b). Mari bahas satu per satu!
Parabola dengan Titik Puncak O (0, 0)
Berikut ini adalah contoh gambar parabola, baik yang bentuknya horizontal ataupun vertikal yang memiliki titik puncak O (0, 0).
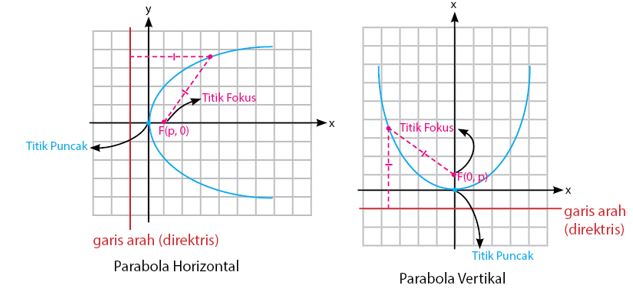
Dari titik puncak tersebut, maka bisa dihasilkan persamaan berikut! (persamaan ini berlaku untuk parabola horizontal ataupun vertikal).
| Keterangan | Parabola Horizontal | Parabola Vertikal |
| Puncak | O (0, 0) | O (0, 0) |
| Fokus | (p, 0) | (0, p) |
| Garis Arah | x = -p | y = -p |
| Persamaan Umum | y2 = 4px | x2 = 4py |
Parabola dengan Titik Puncak P (a, b)
Gambar dari parabola dengan titik puncak pada P (a, b) adalah seperti ini! Setelah gambar, ada bentuk persamaan umumnya baik untuk parabola horizontal atau vertikal.
| Keterangan | Parabola Horizontal | Parabola Vertikal |
| Puncak | P (a, b) | P (a, b) |
| Fokus | (a + p, b) | (a, b + p) |
| Garis Arah | x = a – p | y = b – p |
| Persamaan Umum | (y – b)2 = 4p (x – a) | (x – a)2 = 4p (y – b) |
Terakhir, ada irisan kerucut berupa hiperbola, langsung saja menuju materinya!
4. Irisan Kerucut Hiperbola
Hiperbola tersusun atas beberapa komponen, seperti asimtot, kurva, garis arah, titik puncak, titik fokus, dan sebagainya. Komponen-komponen tersebut memiliki keterkaitan satu sama lain. Sehingga, ada rumus yang harus kamu perhatikan. Hiperbola ada dua jenis, yakni vertikal dan horizontal.
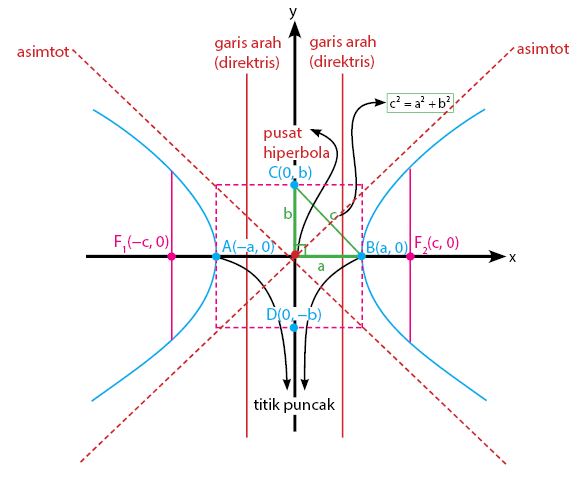
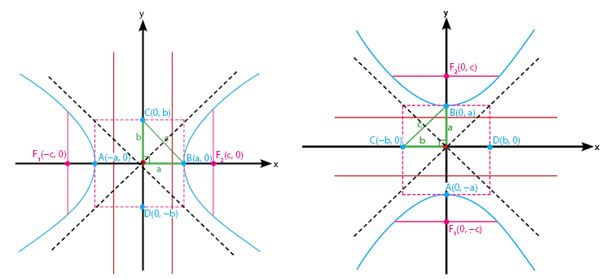
hiperbola horizontal
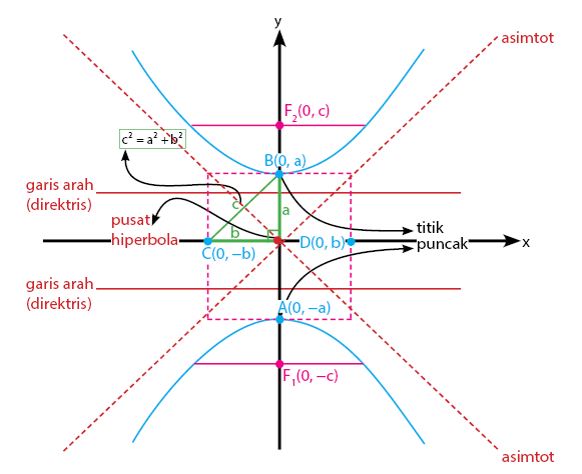
hiperbola vertikal
Hiperbola juga dibedakan dari pusatnya, ada yang pusatnya terletak pada titik O (0,0), serta ada juga yang pusatnya ada di P (a, b).
Persamaan pada Hiperbola pada pusat O (0,0)
Gambar hiperbola pada pusat O (0,0) adalah sebagai berikut:
| Keterangan | Bentuk Elips Horizontal 1 | Bentuk Elips Horizontal 2 |
| Pusat | O (0, 0) | P (p, q) |
| Fokus | (+ c, 0) | (0, +c) |
| Puncak | (+a, 0) | (0, +a) |
| Bentuk umum persamaan | x2/a2 – y2/b2 = 1 | x2/b2 – y2/a2 = 1 |
| Gari arah atau direktris | X = + a2/c | X = p + a2/c |
| Panjang Loctus Rectum | LR = |2b2/a| | LR = |2b2/a| |
| Eksentrisitas | e = c/a | e = c/a |
| Asimtot | Y = + b/a | Y = + b/a |
Nah, cukup sampai sini dulu, ya! Kamu bisa aktif mencari contoh soalnya sendiri lalu kerjakan dengan panduan materi di atas.
Semoga mudah dipahami dan membantu kamu menyelesaikan soal-soal tentang irisan kerucut!

