Rumus Mean, Median, Modus serta Contoh Soal dan Pembahasannya

Mean, Median, Modus – Beberapa diantara kalian mungkin sudah cukup familiar dengan istilah ukuran pemusatan data. Tapi sudahkan kamu tahu apa definisi dari istilah tersebut? Ukuran pemusatan data ialah sembarang ukuran yang memperlihatkan pusat segugus data, serta sudah diurutkan baik dari yang terkecil hingga yang terbesar ataupun sebaliknya.

Salah satu fungsi dari ukuran pemusatan data ialah untuk membandingkan dua populasi atau lebih. Biasanya ukuran pemusatan data digunakan karena sulitnya membandingkan masing-masing anggota dari anggota populasi atau data.

Nilai statistik dari ukuran pemusatan data dibuat sedemikian rupa agar dapat mewakili seluruh nilai pada data yang diterangkan/bersangkutan. Disini, mean, modus dan median adalah nilai statistik yang bisa menggambarkan suatu data. Dimana data-data umumnya dibagi dalam 2 jenis, yakni data tunggal dan juga data berkelompok.

Rumus Mean, Median, Modus

Untuk mencari nilai dari mean, media dan modus pada data tunggal memang bisa dilakukan secara mudah, atau bahkan tanpa rumus sekalipun. Tapi lain halnya jika kamu ingin mencari mean, median atau modus pada data berkelompok.

Dimana penyajian data dilakukan berkelompok, sehingga untuk mencari nilai mean, median atau modusnya pun dibutuhkan rumus tersendiri, berikut ini tabel ringkasannya.

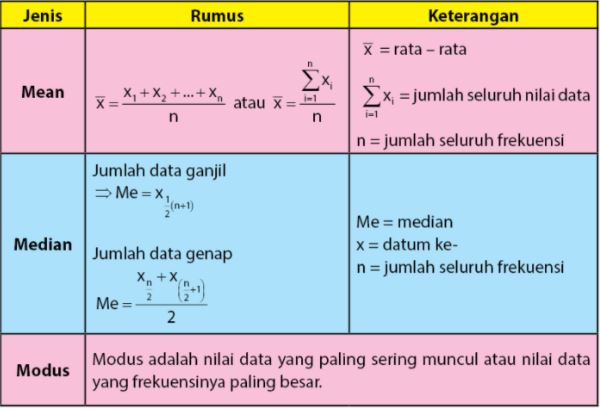
Mean Median Modus Data Kelompok

Data berkelompok sendiri bisa disajikan dalam bentuk diagram batang, distribusi frekuensi, dan lain sebagainya. Nah, berikut ini contoh dari penyajian data berkelompok.

1. Penyajian data berkelompok dalam bentuk tabel

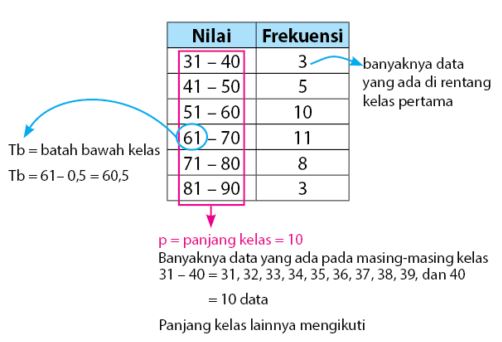
2. Penyajian data berkelompok dalam bentuk diagram batang

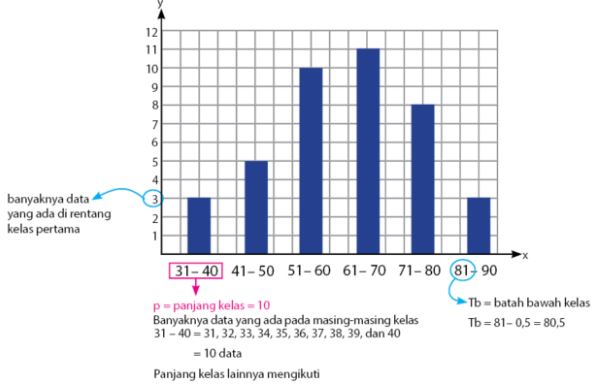
Dari contoh penyajian data di atas, bisa dilihat beberapa nilai yang terkelompok. Lalu bagaimana cara menentukan mean, median dan modus dari bentuk data seperti di atas?

Mean (Rataan)

Mean atau rataan adalah nilai rata-rata dari beberapa data. Nilai mean pun dapat dicari dari berbagai jenis data, baik data tunggal maupun data berkelompok. Untuk mencari nilai mean data tunggal, bisa ditentukan dengan cara menjumlahkan seluruh data kemudian membaginya sesuai jumlah data tersebut.

Hanya saja, cara mencari mean pada data berkelompok sedikit lebih rumit sehingga kamu harus menggunakan rumus matematika.

Berikut ini rumus mean data berkelompok:

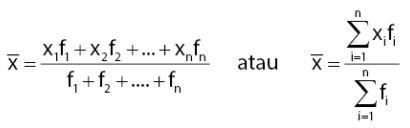
Keterangan:

• x̄ = rataan hitung dari data kelompok
• f_i= frekuensi kelas ke-i
• x_i= nilai tengah kelas ke-i

Median (Data Tengah)

Media ialah data tengah yang didapatkan setelah seluruh data diurutkan. Untuk mencari media pada data tunggal, kamu bisa menggunakan cara manual yakni dengan mengurutkan data kemudian mencari data yang terletak di tengah.

Sama seperti pada data tunggal, media pada data berkelompok juga merupakan data yang letaknya berada di tengah. Hanya saja, karena penyajian datanya dalam bentuk kelompok maka data tidak bisa diurutkan seperti pada data tunggal.

Oleh karena itu, untuk mencari median pada data berkelompok pun dibutuhkan rumus. Berikut adalah rumus median data kelompok dan keterangannya.

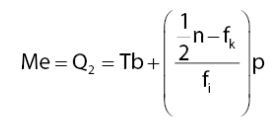
Keterangan:

• T_b= tepi bawah kelas median
• n = jumlah seluruh frekuensi
• f_k = jumlah frekuensi sebelum kelas median
• f_i= frekuensi kelas median
• p = panjang kelas interval

Umumnya, data kelompok dibagi dalam empat bagian yang sama banyak. Pembagian data dalam empat kelompok ini akan dipisahkan menggunakan tiga kuartil, yakni kuartil atas (Q₁), kuartil tengah (Q₂), dan juga kuartil bawah (Q₃).

Dari penjelasan di atas, bisa disimpulkan jika median adalah data ke-n yang membagi banyak data dalam dua kelompok sama banyak. Begitu juga juga dengan Q₂, sehingga nilai dari median sama dengan kuartil dua.

Modus (Niat yang Paling Sering Muncul)

Modus merupakan nilai data yang paling kerap muncul. Dengan kata lain, modus ialah data yang memiliki nilai frekuensi tertinggi. Untuk mencari modus pada data tunggal caranya sangat mudah, kamu hanya perlu mencari data yang paling sering muncul atau yang frekuensinya paling tinggi. Caranya pun bisa dilakukan secara manual dengan mengecek satu persatu data tunggal yang tersaji.

Tapi bagaimana jika pada data berkelompok? Tentu tidak semudah itu, karena penyajian data berkelompok dibuat dalam rentang kelas. Jadi, nilai modus dari data kelompok pun tidak bisa ditentukan langsung dengan melihat data yang paling sering muncul.

Kamu bisa menggunakan rumus berikut untuk menentukan nilai modus pada data berkelompok. Adapun penjelasan rumus modus data kelompok adalah sebagai berikut.

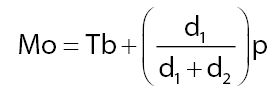
Ketarangan:

• Tb = tepi bawah kelas modus
• d₁ = selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus
• d₂ = selisih frekuensi kelas modus dengan frekuensi setelah kelas modus
• p = panjang kelas interval

Contoh Soal Mean, Median dan Modus

Agar lebih paham dengan materi yang kita pelajari kali ini, yuk simak pembahasan mengenai contoh soal mean, median dan modus yang ada dibawah ini.

1. Contoh Soal Mean

Tentukan mean dari data di bawah ini:

Nilai	Frekuensi
31-40	3
41-50	5
51-60	10
61-70	11
71-80	8
81-90	3

Jawab:

Sebelumnya, kita membutuhkan nilai tengah dari masing-masing kelas untuk bisa menentukan nilai rata-rata kelompok. Nilai tengah dari masing-masing kelas bisa didapatkan dengan menggunakan rumus:

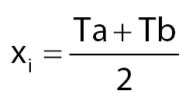
Maka nilai tengah dari masing-masing kelas adalah sebagai berikut:

Hasil perkalian nilai tengah dari masing-masing kelas dan frekuensinya bisa dilihat dalam tabel berikut.

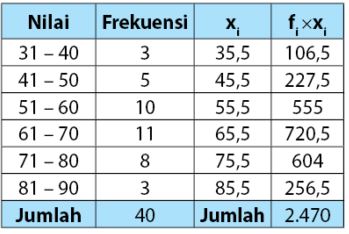
Sehingga

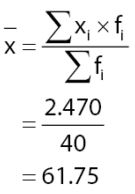
Jadi mediannya adalah 61.75

2. Contoh Soal Median

Tentukan median dari data di bawah ini:

Nilai	Frekuensi
31-40	3
41-50	5
51-60	10
61-70	11
71-80	8
81-90	3

Jawab:

Diketahui jumlah data pada tabel adalah 40, sehingga letak median berada di data: Q₂ = ½ × 40 = 20  (letak median di data ke-20).

Tapi sebelum menentukan nilai media dari data di atas, kita tentukan frekuensi kumulatif dari dan letak kelas dimana data median berada. Gunakan tabel pembantu ini:

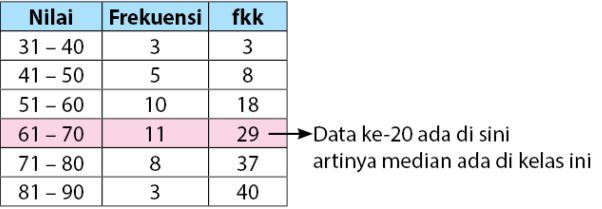
Informasi yang diperoleh dari tabel di atas adalah:

• Tb = 61 – 0,5 = 60,5
• p = 10
• f_kk= 18
• f_i = 11

Untuk menghitung median data berkelompok di atas kamu bisa mengikuti langkah-langkah berikut.

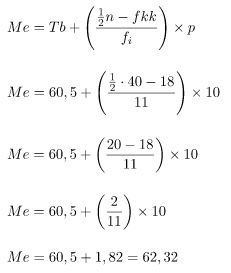
Jadi, nilai mediannya adalah 62,32

3. Contoh Soal Modus

Tentukan modus dari diagram batang di bawah ini.

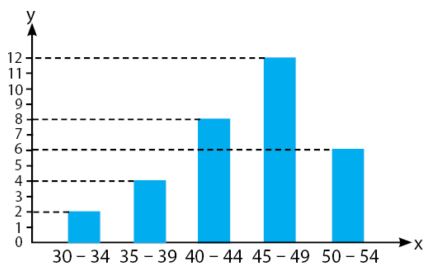
Jawab:

Dari diagram batang di atas, diketahui modus berada pada interval 45-49, sehingga:

T_b = 45 – 0,5 = 44,5
d₁ = 12 – 8 = 4
d₂ = 12 – 6 = 6

Maka nilai modus dari data di atas adalah:

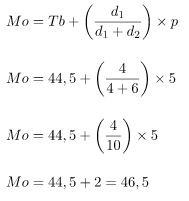
Dengan menggunakan rumus-rumus mean, median dan modus di atas, kamu bisa menentukan nilai yang diinginkan secara lebih cepat dan pastinya akurat.

Mengingat tidak semua data disajikan dalam bentuk tunggal, dan justru lebih banyak disajikan dalam bentuk kelompok agar informasi yang disampaikan lebih jelas dan mudah dibaca.

Rumus matematika tersebut juga bisa diaplikasikan dalam kehidupan sehari-hari, dan pastinya sangat membantu.

Selamat belajar dan semoga informasi di atas membantu ya!