Pembahasan Persamaan Trigonometri serta Contoh Soalnya

Persamaan trigonometri adalah jenis persamaan yang memuat fungsi trigonometri pada sudut yang nilainya belum diketahui. Kalau kamu sudah pernah mempelajari tentang persamaan kuadrat atau persamaan linear, sebetulnya, persamaan trigonometri tidak jauh beda. Hanya saja, himpunan penyelesaian di persamaan trigonometri ini adalah dalam bentuk besaran sudut.

Pada materi ini, nantinya kamu akan mempelajari tiga jenis persamaan trigonometri yang sederhana. Untuk menyelesaikan materi ini, kamu akan diminta untuk mencari semua nilai dari sudut x, sehingga, persamaan akan bernilai benar bagi daerah asalnya. Apa sajakah tiga persamaan tersebut?

Ya, betul sekali, ada persamaan sinus, cosinus, serta tangen. Untuk materi kali ini akan dibatasi untuk penyelesaian pada rentang dari 0^o hingga 360^o atau antara 0 hingga 2π. Langsung saja, kita masuk ke rumusnya!

Rumus Persamaan Trigonometri

Untuk menyelesaikan persamaan trigonometri, tentu saja kamu haru tahu rumusnya terlebih dahulu. Kamu catat dan ingat baik-baik rumus berikut ini, ya! Karena rumusnya cukup banyak, sebaiknya kamu sering melakukan latihan agar lebih mudah hafal.

Ingat, untuk memahami materi trigonometri yang perlu kamu lakukan adalah banyak berlatih dengan metode yang benar. Tanpa Latihan, rumus yang sudah dihafalkan tidak akan bermanfaat dengan baik ketika kamu mengerjakan ujian nanti.

Rumus Persamaan Sinus

Pertama, kamu bisa menyimak rumus persamaan sinus terlebih dahulu. Nah, untuk menyelesaikan soal trigonometri, biasanya, akan diberikan informasi mengenai nilai lebih dari satu sudut. Sebab, grafik fungsi trigonometri akan memuat nilai yang sama pada beberapa sudut. Seperti pada persamaan y = sin x, -360^o < x < 360^o. Apabila digambarkan pada suatu grafik, maka persamaan tersebut akan jadi:

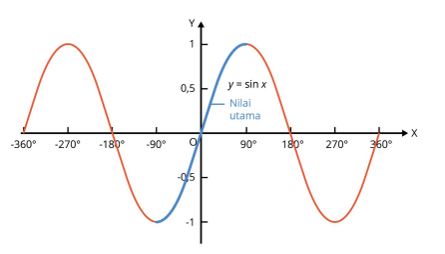
Pada grafik ditunjukkan nilai x pada persamaan sin x = 1 ada dua hasil penyelesaian, yakni -270^o serta 90^o. Lalu, untuk menentukan nilai yang lain, kamu bisa memakai rumus persamaan trigonometri.

Berikut rumusnya!

Rumus dalam derajat

sin x = sin α

x₁ = α + k . 360^o

x₂ = (180^o – α) + k . 360^o

Rumus dalam radian

sin x = sin α

x₁ = α + k . 2π

x₂ = (π – α) + k . 2π

Keterangan k € bilangan bulat

Penerapan rumus persamaan sinus ini bisa langsung kamu lihat melalui contoh berikut ini!

Silakan kamu tentukan penyelesaian dari persamaan pada  interval 0 < x < 2π!

Jawab :

Dari contoh soal dan pembahasan di atas, kamu bisa mencari x terlebih dahulu, kemudian akan ditemukan himpunan penyelesaiannya.

Rumus Persamaan Cosinus

Selanjutnya persamaan cosinus. Persamaan ini bisa diselesaikan dengan melihat grafik yang sudah tersedia. Selanjutnya kerjakan sesuai dengan keterangan pada grafik.

Untuk persamaan trigonometri dalam bentuk cosinus, kamu bisa melihat grafik ini terlebih dahulu!

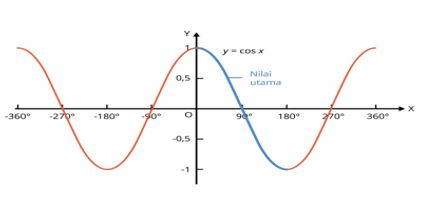
Silakan kamu lihat nilai utama yang ditunjukkan oleh garis biru tersebut. Lebih tepat lagi, nilai utama tersebut ada pada interval 0^o < x < 180^o. Sedangkan nilai cosinus lainnya dapat kamu hitung melalui rumus berikut ini!

Rumus Persamaan Cosinus

Rumus dalam derajat

cos x = cos α

x = + α + k. 360^o

Rumus dalam radian

cos x = cos α

x = + α + k. 2π

Bagaimana kalau kamu langsung masuk ke contoh soalnya saja? Baik lah, mari kita mulai!

Cari lah penyelesaian dari persamaan pada interval 0^o < x < 360^o

Penyelesaian:

Rumus Persamaan Tangen

Persamaan tangen merupakan persamaan trigonometri yang berisikan fungsi tangen. Biar kamu lebih jelas, coba perhatikan grafik dari persamaan y = tan x pada interval -360^o < x < 360^o.

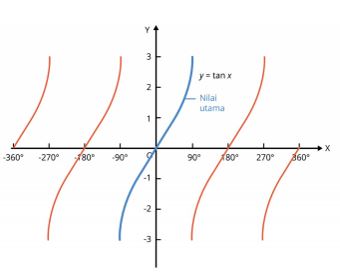
Setelah melihat nilai utama yakni pada garis biru, atau lebih pada interval -90^o≤ x ≤ 90^o, maka kamu akan tahu jika nilai itu akan berulang bagi x positif dan juga x negatif.

Lalu bagaimana cara menyelesaikan persoalan terkiat persamaan tangen? Kamu bisa menggunakan rumus, untuk mencari nilai yang lain, silakan kamu tentukan menggunakan rumus persamaan trigonometri berikut ini!

Rumus Persamaan Tangen

Persamaan dalam Derajat

tan x = tan α

x = α + k. 180^o

Persamaan dalam Radian

tan x = tan α

x = α + k. 2π

Langsung saja, kita masuk ke contoh soalnya, ya!

Cari lah penyelesaian dari persamaan berikut pada interval 0 ≤ x ≤ 2π! Persamaan:

Penyelesaian

Contoh Soal Persamaan Trigonometri

Siapa bilang belajar tentang persamaan trigonometri tidak berguna di kehidupan sehari-hari? Kalau kamu beranggapan demikian, artinya, salah besar. Nyatanya masih banyak kejadian sehari-hari yang berkaitan erat dengan persamaan trigonometri, termasuk permasalahan-permasalahan yang bisa diselesaikan dengan mudah menggunakan rumus-rumus di atas.

Ada banyak masalah dalam kehidupan yang bisa diselesaikan menggunakan rumus-rumus tersebut. Beberapa diantaranya untuk mencari periode gelombang cahaya serta gelombang bunyi.

Selain itu, persamaan trigonometri juga bisa digunakan untuk menentukan kecepatan sudut partikel. Nah, partikel yang mempunyai kecepatan sudut tentu saja persamaan geraknya akan sesuai dengan persamaan trigonometri.

Penasaran bagaimana penyelesaiannya? Yuk, simak beberapa contohnya di bawah ini!

Contoh Soal 1

Persamaan gerak partikel diketahui sebagai : S = A cos (ωt), t ≥ 0. Dikarenakan pergerakan ini terjadi ketika t ≠ 0, sehingga, persamaannya menjadi S = A cos (ωt), t > 0. Simpangannya adalah 1 satuan serta memiliki amplitudo √2, sehingga menjadi:

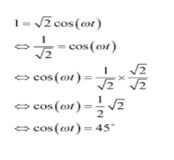
Maka, artinya:

Contoh Soal 2

Tentukan himpunan penyelesaian dari cos x = ½ untuk 0^o < x < 360^o!

Jawab :

½ merupakan nilai cosinus dari 60^o, maka persamaannya diubah menjadi :

cos x = cos 60^o

Sesuai dengan rumus, bahwa cos x = cos α, maka:

x = α + k . 360

X = – α + k . 360

1. x = 60^o + k . 360^o

k = 0 => x = 60 + 0 = 60^o

k = 1 => x = 60 + 360 = 420^o

2. x = -60^o + k . 360^o

k = 0 => x = 60 + 0 = 60^o

k = 1 => x = -60 + 360 = 300^o

Maka, himpunan penyelesaiannya adalah = {60^o, 300^o}

Contoh Soal 3

Dari persamaan cos 2x + sin x = 0, 0 < x < 2π, tentukan himpunan penyelesaiannya!

Jawab :

Berdasarkan rumus sudut rangkap, yakni

cos 2x = cos² x – sin² x

cos 2x = 2 cos² x – 1

cos 2x = 1 – 2 sin² x, maka persamaannya menjadi :

cos 2x + sin x = 0

1 – 2 sin² + sin x = 0

-2 sin² x + sin X = 0

2 sin² x – sin x – 1 = 0

Kemudian, difaktorkan menjadi :

(2 sin x + 1) (sin X – 1) = 0

2 sin x + 1 = 0

2 sin x = -1

sin x = – ½

x = 210^o dan x = 330^o

atau bisa menjadi

sin x – 1 = 0

sin x = 1

x = 90^o

Maka, himpunan penyelesaiannya menjadi :

HP {90^o, 210^o, 330^o}, atau {π/2, 7π/6, 11π/6}

Nah, itulah beberapa rumus dan pembahasan serta contoh soal persamaan trigonometri yang sifatnya sederhana. Materi ini adalah pelengkap dalam seluruh kesatuan topik tentang trigonometri. Kunci dari memahami materi ini adalah sering-sering berlatih. Kamu pun tidak perlu lagi sulit-sulit menghafalkan rumus jika sudah sering mengerjakan soal. Sebab, kamu bisa hafal dengan sendirinya. Selamat belajar!