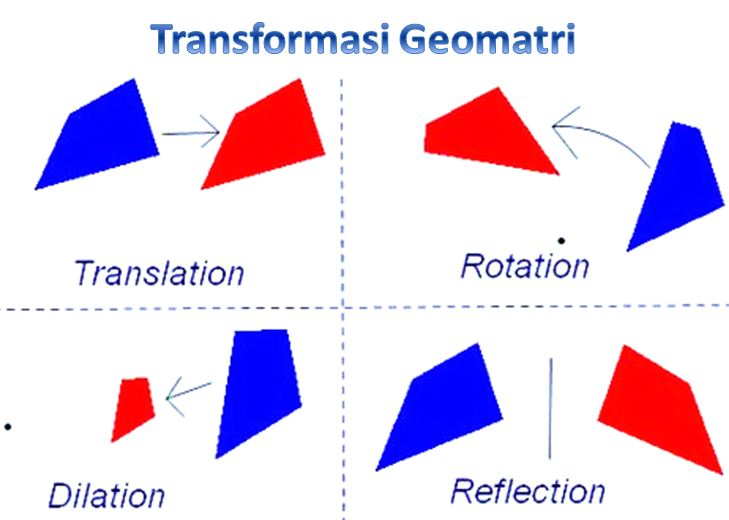
Transformasi Geometri – Pelajaran matematika ternyata memiliki manfaat yang sangat besar lho bagi kehidupan sehari-hari. Tidak sesederhana perhitungan jual-beli saja, seperti penjumlahan atau persamaan linear dan pertidaksamaan linear, namun matematika juga sangat penting dalam ilmu arsitektur.

Pengertian Transformasi Geometri

Secara bahasa arti transformasi geometri adalah perubahan. Secara lengkapnnya pengertian transformasi geometri adalah perubahan pada sebuah bidang geometri yang mencantum posisi, besar dan bentuknya sendiri.

Bagi kamu yang memiliki cita-cita jadi arsitek, harus banget menyimak ulasan kali ini. Sebab, artikel ini akan membahas tentang transformasi geometri. Apa sih, hubungannya? Nah, pastinya, kamu sudah pernah melihat gedung pencakar langit dan ingin tahu gimana caranya gedung yang menjulang tinggi itu tetap kokoh walaupun terkena oleh angin kencang sekalipun.

Di sini lah pentingnya seorang arsitek menguasai transformasi geometri. Apa alasannya dan apa sebetulnya transformasi geometri itu? Yuk, cari tahu di ulasan ini!

Konsep Transformasi Geometri

Tahukah kamu kalau konsep ini dilahirkan oleh seorang matematikawan bernama Felix Klein yang lahir di tahun 1849. Saat ia berusia 23 tahu, Felix mengungkapkan jika bangun geometri bisa diubah bentuk dan letaknya. Maka dari itu, terdapat perubahan letak maupun bentuk dari bangun geometri itu sendiri.

Ada beraneka macam bangun geometri, mulai dari segitiga, persegi, lingkaran, limas, dan sebagainya. Tak hanya itu saja, bahkan titik dan garis juga bisa ditransformasikan. Sebab, bangun ruang sendiri merupakan kumpulan garis yang terhubung satu sama lain dengan sistematis. Sedangkan garis adalah kumpulan titik yang terhubung satu sama lain dengan sistematis.

Mengapa arsitek memerlukan ilmu transformasi geometri ini? Sebab, arsitek harus punya kemampuan menempatkan objek berupa bangunan pada titik tertentu secara presisi dan akurat. Semisal, saat arsitek ini akan menempatkan bangunan supaya tidak terpapar sinar matahari langsung.

Jadi, bangunan harus ditranslasi atau digeser, atau ditempatkan berapa meter dari lokasi yang sebelumnya supaya tidak terkena matahari langsung. Juga, perlu atau tidaknya bangunan diperkecil sesuai dengan tanah yang tersedia? Semua jawabannya ada di materi transformasi geometri ini. So, siap untuk pembahasannya?

Jenis Transformasi Geometri

Ada beberapa jenis transformasi geometri. Apabila hasil dari transformasi secara kongruen dengan bangunan, maka, jenis ini adalah transformasi isometri. Transformasi isometri dibagi lagi menjadi dua jenis, yakni langsung dan berhadapan. Yang termasuk dalam transformasi isometri langsung adalah translasi dan rotasi. Sedangkan untuk transformasi isometri berhadapan terdiri dari refleksi.

Yuk, bahas satu per satu!

Translasi

Pengertian dari transalasi adalah pergeseran maupun pemindahan semua titik di bidang geometri dengan arah dan jarak yang sma. Notasi atau penulisan translasi tidak berbeda dengan notasi untuk vektor. Apabila titik B ditranslasikan hingga B^I, bisa dinotasikan sebagai:

Contoh transformasi geometri yang satu ini adalah:

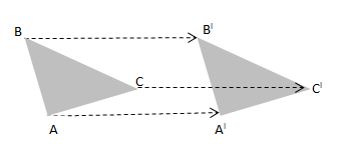
Jika kamu lihat gambar, maka masing-masing A, B, serta C ditranslasikan pada titik A^I, B^I, C^I yang memiliki jarak serta arah yang sama.

Nah, di suatu proses translasi bisa ditinjau pada sumbu x serta y. Jarak pergeseran a akan sejajar dengan sumbu x, jika bergeser ke arah kanan, maka a > 0, sedangkan jika ke kiri, maka a< 0. Untuk pergeseran dengan jarak b, maka, akan sejajar dengan sumbu y. Apabila pergeseran ke arah atas, maka b > 0, apabila ke bawah, maka b < 0, maka bisa dinyatakan dengan:

Dimana a dan b merupakan komponen translasi. Untuk bentuk translasi sejauh (a/b) adalah sebagai berikut:

Translasi Titik

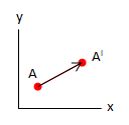
Dengan posisi awal A (x, y), maka rumus posisi akhirnya akan menjadi A^I ( x + a, y + b) dimana x dan y merupakan koordinat.

Translasi Garis

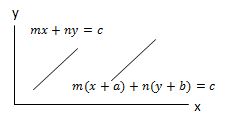
Posisi awalnya adalah mx + ny = c, maka, rumus posisi akhirnya menjadi m (x + a) + n (y + b) = c. Dimana m dan n merupakan koefisien, sedangkan c merupakan konstanta.

Translasi Kurva

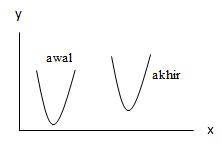
Posisi awalnya adalah y = mx² + kx + l, maka posisi akhirnya menjadi (y + b) = m (x + a)² + k (x + a) + l. Dimana m dan k merupakan koefisien, sedangkan l adalah konstanta.

Translasi Lingkaran

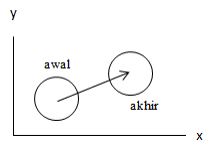
Dengan posisi awal x² + y² = c, maka posisi akhirnya menjadi (x + a)² + (y + b)² = c. Dengan c merupakan konstanta.

Refleksi

Refleksi adalah jenis transformasi geometri dimana pergeseran semua titik di bidang geometri menuju ke arah garis (cermin) dengan jarak yang sama serta dua kali jarak dari titik ke cermin. Terdapat dua sifat yang perlu kamu perhatikan dari refleksi ini, yakni:

Jarak titik dan cermin sama dengan jarak dari bayangan ke cermin.
Geometri yang dicerminkan akan berhadapan dengan petanya.

Biar lebih paham, kamu bisa lihat gambar ini:

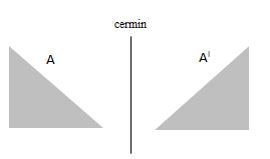
Beberapa bentuk refleksi bisa kamu lihat di bawah ini!

Refleksi Terhadap Sumbu Y

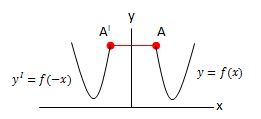
Titik awal A (x, y) memiliki bayangan A^I (-x, y). Sedangkan untuk garis ataupun kurva y = f (x), akan memiliki bayangan y^I = f(-x).

Refleksi Terhadap Sumbu y = h

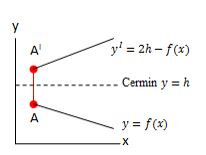
Titik awal A (x, y) yang direfleksikan, akan memiliki bayangan pada titik A^I (x, 2h – y). Sedangkan untuk garis atau kurva y = f (x), bayangannya ada di y^I = 2h – f(x).

Refleksi Terhadap Sumbu x = h

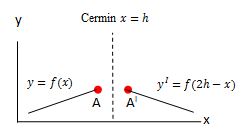
Titik awal A ( x, y) yang direfleksikan, akan memiliki bayangan pada titik A^I (2h – x, y). Sedangkan untuk garis atau kurva y = f (x), bayangannya ada di y^I = f(2h – x).

Refleksi Terhadap Sumbu y = x

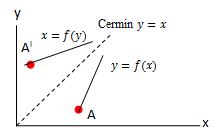
Titik awal A ( x, y) yang direfleksikan, akan memiliki bayangan pada titik A^I (y, x). Sedangkan untuk garis atau kurva y = f (x), bayangannya ada di x = f(y).

Refleksi Terhadap Sumbu y = -x

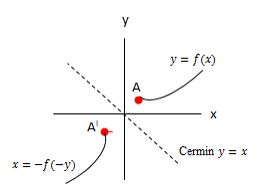
Titik awal A ( x, y) yang direfleksikan, akan memiliki bayangan pada titik A^I (-y, -x). Sedangkan untuk garis atau kurva y = f (x), bayangannya ada di x = -f(-y)

Refleksi pada Titik 0 (0, 0)

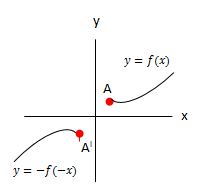
Titik awal A ( x, y) yang direfleksikan, akan memiliki bayangan pada titik A^I (-x, -y). Sedangkan untuk garis atau kurva y = f (x), bayangannya ada di y^I = -f(-x).

Rotasi

Pernah mendengar tentang rotasi? Ya, betul, kata ini biasa disebut pada pelajaran geografi. Rotasi bumi adalah perputaran bumi pada porosnya. Nah, konsepnya juga tidak berbeda. Rotasi adalah transformasi geometri berupa pemindahan atau pergeseran semua titik di bidang geometri yang ada di sepanjang busur lingkaran dengan titik rotasi berupa titik pusat lingkaran.

Rotasi bernilai positif apabila arahnya berlawan dengan jarum jam, tetapi bernilai negatif apabila searah dengan jarum jam. Contohnya adalah:

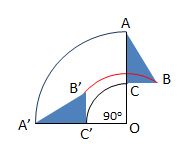
Bentuk rotasi sendiri bisa kamu lihat di tabel berikut!

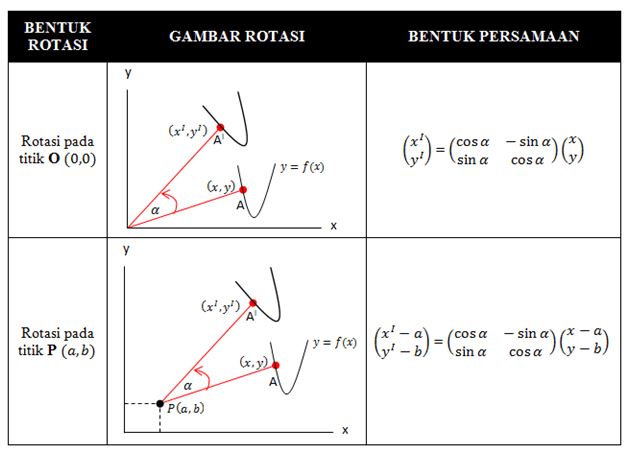
Dilatasi

Terakhir, ada dilatasi yang merupakan bentuk transformasi geometri yang berupa perbesaran atau perkecilan bangunan geometri. Pada konsep dilatasi, terdapat titik dilatasi serta faktor dilatasi.

Titik dilatasi akan menentukan posisi perubahan. Dimana ini akan jadi titik pertemuan dari semua garis lurus yang menghubungkan titik pada suatu bangun pada titik-titik hasil dari dilatasi.

Dilatasi bisa ditulis sebagai (D, k) = (titik dilatasi, faktor dilatasi).

Itulah pembahasan tentang transformasi geometri. Pastikan kamu menyimak baik-baik setiap materinya. Selamat belajar!

Transformasi Geometri