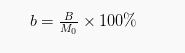Bunga Tunggal, Majemuk dan Anuitas – Ketika membicarakan tentang perbankan, mungkin yang pertama akan terbesit dalam pikiran kamu adalah mata pelajaran ekonomi atau akuntansi. Tapi, ilmu ekonomi pun tidak jauh-jauh dari hitung-hitungan matematika. Contohnya saja untuk menghitung bunga tunggal.
Pasti kamu pernah mendengar bunga bukan? Namun dalam konteks ini, bunga yang dimaksud bukanlah bunga tanaman yaa, akan tetapi bunga pertambahan nilai dalam matematika bisnis. Pehitungan bunga, baik bunga tunggal, majemuk dan anuitas, semuanya menggunakan konsep baris dan juga deret. Oleh sebab itu, kamu juga harus mempahami terlebih dahulu materi tersebut ya.
Bunga dalam Matematika
Bunga atau bank interest (suku bunga) merupakan pertambahan nilai pada jumlah modal yang diberikan bank kepada para nasabahnya, yang mana besar kecilnya bunga ditentukan oleh persentase modal dan waktu seberapa lama nasabah menabung.
Selain diberikan kepada yang menabung, bunga atau suku bunga pada umumnya juga dapat diberikan dari pemberi pinjaman kepada peminjam. Bank interest ada dua jenis, yakni bunga tunggal serta bunga majemuk. Apasih perbedaan keduanya? Simak informasinya di bawah ini:
Bunga Tunggal
Apa itu bunga tunggal? Pengertian bunga tunggal adalah bunga yang ditentukan dari besaran modal awal, sehingga bunga yang diberikan hanya satu jenis saja atau tetap, dari periode awal hingga berakhirnya periode tersebut.
Contoh bunga tunggal adalah, ketika menabung di bank, kita biasanya mendapatkan bunga dengan persentase yang tetap pada setiap periodenya kan?
Selanjutnya, apa yang dimaksud dengan modal? Modal adalah jumlah uang yang disetorkan pada awal periode dan merupakan jumlah yang dibungakan. Sedangkan modal awal merupakan modal pada periode awal sebelum nantinya dibungakan.
Kemudian modal akhir merupakan hasil akhir dari modal yang telah dibungakan. Dan suku bunga adalah besarnya bunga yang berbentuk persentase pada tiap satuan waktu.
Rumus Bunga Tunggal
Apabila modal awal sebesar M0 dan mendapatkan bunga tunggal sebanyak b (dalam bentuk persentase) setiap bulannya, sehingga setelah sebanyak n bulan besar modal akhirnya Mn menjadi:
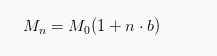
1. Contoh Soal Bunga Tunggal
Diketahui modal pinjaman sebuah bank Rp. 1.500.000 dengan bunga 2% per bulan, maka setelah 6 bulan modalnya menjadi …
Mn = 1.500.000 (1 + 6 x 2%) = Rp. 1.680.000,-
Apabila modal awal sebanyak M0, serta diketahui banyak bunga tunggalnya B, sehingga persentase bunga tunggalnya adalah b.
2. Contoh soal bunga tunggal
Jika diketahui bunga tunggalnya adalah Rp. 20.000,- untuk modal pinjaman sebesar Rp. 800.000,-. Sehingga persentase bunganya adalah …
b= x 100% = 2,5%
Bunga Majemuk
Apa itu bunga majemuk? Pengertian bunga majemuk adalah bunga yang diberikan, dimana bunga tersebut berdasarkan modal awal serta akumulasi dari bung pada periode sebelumnya. Berbeda dengan bunga tunggal yang tetap tidak berubah-ubah, bunga majemuk memiliki begitu banyak variasi serta tidak tetap dan selalu berubah-ubah tiap bulan atau periodenya.
Contoh bunga majemuk adalah, ketika menjual kendaraan, harga jual kendaraan yang akan dijual selalu beruah setiap periode serta jumlah perubahaannya bervariasi. Perhatikan gambar di bawah ini!
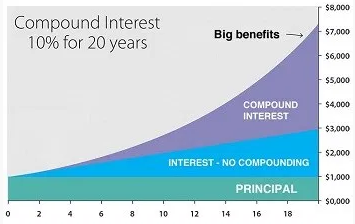
Rumus Bunga Majemuk
Apabila modal awal sebanyak M0 dan mendapatkan bunga majemuk sebanyak b (persen) perbulan, sehingga setelah n bulan banyaknya modal Mn, menjadi:
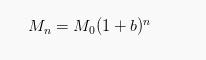
1. Contoh soal bunga majemuk
Diketahui modal sebuah pinjaman Rp. 2.000.000 dengan bunga majemuk sebanyak 2% setiap bulannya, sehingga setelah 5 bulan modalnya menjadi….
Mn = 2.000.000 (1 + 0,02)5 = 2.208.161,60
Apabila modal awal sebanyak M0 ditabung di bank dan mendapatkan bunga sebanyak b per bulan, kemudian banyaknya bunga dihitung sebanyak m kali dalam kurun waktu satu tahun, sehingga besarnya modal pada akhir tahun ke n yaitu:
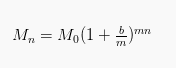
2. Contoh soal bunga majemuk
M0 = 2.000.000
m = 12 kali
n = 3 tahun
b = 5%
Sehingga,
Mn= 2.000.000 (1 + ) 12×3 = 2,101.151, 68
Bunga Anuitas
Apa itu bunga Anuitas? Pengertian bunga anuitas adalah sebuah rangkaian pembayaran ataupun penerimaan dengan jumlah yang sama serta dibayarkan ataupun yang harus diterima pada setiap akhir periode sebuah kredit atau pinjaman. Apabila sebuah pinjaman akan dibayarkan secara anuitas, maka ada banyaknya 3 komponen yang menjadi dasar dalam perhitungan, yakni:
- Besarnya pinjaman
- Besarnya bung pinjaman
- Jangka waktu serta jumlah periode pembayaran
Anuitas diberikan secara tetap setiap akhir periodenya, hal ini memiliki dua fungsi yakni mengangsur hutang dan membayar bunga atas hutang tersebut. Sehingga rumusnya menjadi:
Rumus Bunga Anuitas
![]()
Apabila hutang sebanyak Mo dan mendapatkan bunga sebanyak b setaip bulannya dan anuitas sebanyak A, sehingga dapat ditentukan:
- Besarnya bunga pada akhir periode n
Bn = (1 +b)n-1 (b.M – A)+ A
- Besarnya angsuran akhir periode ke-n
An = (1+b) n-1 (A- bM)
- Banyaknya sisa hutang pada akhir periode n
Mn = (1 +b)n (M- ) +
Besarnya anuitas untuk membayar hutang sebesar M0 dan bungan sebanyak b setiap bulannya selama n bulan yaitu:
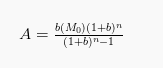
Contoh Soal dan Pembahasan Bunga Tunggal, Majemuk dan Anuitas
Yuk kita bahas tuntas dengan menghadirkan contoh soal dan pembahasan bunga tunggal, majemuk, dan anuitas di bawah ini, dengan menerapkan rumus bunga tunggal, rumus bunga mejemuk, dan rumus anuitas yang telah kita pelajari di atas. Kuy langsung saja, simak cara penyelesaiannya di bawah ini.
1. Contoh Soal Bunga Tunggal dan Penyelesaiannya:
Adapun pembahasan tentang rumus bunga tunggal, akan kita bahas bersama lengkap dengan contoh soal bunga tunggal dan penyelesaiannya di bawah ini.
- Hitunglah besar modal akhir dari Rp. 5.000.000 yang dipinjam selama 1 tahun dnegan bunga tunggal 1% per bulan.
Penyelesaian:
M = M0 (1+12.i)
= 5.000.000 (1+12.1%)
= 5.000.000 + 5.000.000(12%)
= 5.000.000 + 600.000
= 5.600.000
Jadi, besarnya modal akhir setelah 1 tahun yaitu Rp. 5.600.000,-
2. Contoh Soal Bunga Majemuk dan Pembahasannya Matematika
Adapun pembahasan tentang rumus bunga majemuk, akan kita bahas bersama lengkap dengan contoh soal bunga majemuk dan pembahasannya matematika di bawah ini.
Modal sebesar Rp. 20.000.000, dipinjamkan dengan bunga 2% per tahun yang merupakan bunga majemuk. Berapa besar modal pada awal periode ke 3?
Penyelesaian:
Mn = M0(1+b)n
M0 = 20.000.000 (1 + 0,02)2 (n=2, hal ini dikarenakan awal periode ke 3 sama halnya dengan akhir tahun ke 2)
Mn = 20.000.000 (1,02)2
Mn = 20.808.000,-
Sebuah pinjaman sebanyak Rp. 10,000.000 akan dilunasi dengan anuitas tahunan sebanyak Rp. 2.000.000,-. Apabila suku bunga sebesar 5% per tahun, maka besarnya bunga, angsuran dan sisa hutang pada tahun ketiga yaitu…
Penyelesaian:
-
- Bunga
Bn = (1+b)n-1 (b.M – A) + A
Bn = (1+ 0,05) 3-1 (0,05 x 10.000.000 – 2.000.000) + 2.000.000
Bn = (1.05)2 (-1.500.000) + 2.000.000
Bn= – 1.653.750 + 2.000.000
Bn = 346.250
Jadi, besarnya bunga pada tahun ketiga yaitu Rp. 346.250,-
-
- Angsuran
An = (1+)n-1 (A-bM)
An = (1+0,05)3-1 (2.000.000- (0,05). 10.000.000)
An = (1.05)2 (2.000.000 – 500.000)
An = (1.1025) (1.500.000)
An = 1.653.750
Jadi, besar angsuran pada tahun ketiga yaitu Rp. 1.653.750,-
-
- Sisa Hutang
Mn = (1 + b)n (M – ) +
Mn = (1 + 0,05)3 (10.000.000 – ) +
Mn = (1,05)3 (10.000.000 – 40.000.000) + 40.000.000
Mn = (1,157625)(- 30.000.000) + 40.000.000
Mn = – 34.728.750 + 40.000.000
Mn = 5. 271.250
3. Contoh Soal Anuitas dan Penyelesaiannya
Adapun pembahasan tentang rumus anuitas, akan kita bahas bersama lengkap dengan contoh soal anuitas dan penyelesaiannya di bawah ini.
Apabila sebuah pinjaman sebanyak Rp. 850.000.000,- harus dilunasi dengan anuitas sebanyak 6 dan dasar bunga sebesar 4% setiap bulannya, serta pembayan pertama dibayarkan setelah satu bulan. Maka berapa sisa hutang pada akhir bulan ke-5?
Penyelesaian :

Banyaknya sisa hutang pada akhir periode ke lima yaitu

Jadi, itulah materi mengenai bunga tunggal/majemuk dan anuitas. Matematika keungan lebih menyenangkan bukan? Apalagi jika melihat langsung uangnya ya? Hehe
Meskipun tidak secara langsung kamu menghitung uangnya, tapi tetap harus semangat belajar terus-menerus ya!