Program linear adalah salah satu metode untuk menentukan solusi optimal atas permasalahan linear. Pada program linear, ada yang namanya fungsi objektif serta fungsi tujuan. Batas, syarat, serta kendala pada program linear ini adalah bentuk dari pertidaksamaan linear. Bentuk umum dari pertidaksamaan linear biasanya ax + by < c.
Materi Program Linear dalam Model Matematika
Program linear sebetulnya ada di berbagai bidang seperti ekonomi, teknik optimasi industri, dan juga matematika. Dalam ilmu matematika sendiri, program linear dinyatakan dalam bentuk kalimat pernyataan umum. Selanjutnya diubah dalam bentuk matematika. Dimana pernyataan diubah dalam bentuk notasi matematika.
Supaya kamu mudah memahaminya, kita buat ilustrasi saja, ya! Misalnya, ada produsen makanan yang membuat dua jenis makanan dengan 2 bahan berbeda. Dimana komposisi jenis makanan pertama yang terdiri atas 200 gram bahan a dan 150 gram bahan b. Sementara itu, jenis makanan yang kedua terdiri atas 180 gram bahan a dan 170 gram bahan b.
Di gudang, tersedia 72 kg bahan x dan 64 kg bahan y. Sementara itu, harga jenis makanan yang pertama Rp 500.000,- dan untuk jenis kedua adalah Rp 400.000,-.
Maka, peubah jumlah optimal atas jenis makanan pertama adalah x sementara untuk jenis kedua adalah y. Sehingga, hasil penjualan yang optimal bisa dijadikan bentuk f(x, y) = 500.000 x + 400.000 y. Syaratnya adalah :
- Bahan a maksimal digunakan sebanyak 72.000 gram, sehingga pertidaksamaannya menjadi 200 x + 180y <000
- Bahan b maksimal adalah 64.000 gram, sehingga pertidaksamaannya adalah 150x + 170y <000
Jadi, untuk mendapatkan nilai maksimum f(x,y) = 500.000 x + 400.000y, maka syarat berdasarkan ilustrasi adalah :
200x + 180y < 72.000
150x + 170y < 64.000
x > 0
y > 0
Cara Menyelesaikan Program Linear
Untuk bisa melakukan optimasi pada program linear, kamu bisa mengikuti langkah-langkah berikut ini.
- Menentukan variabel kendala
- Menentukan fungsi tujuan
- Menyusun model variabel kendala
- Menggambar grafik atas model variabel yang sudah susun
- Menentukan titik potong pada grafik yang sudah dibuat
- Menentukan daerah penyelesaian
- Menghitung nilai optimal fungsi tujuan
Nilai Optimal Fungsi Objektif
Langkah terakhir dalam melakukan optimasi program linear adalah menghitung nilai optimal fungsi tujuan. Dimana fungsi objektif adalah fungsi linear serta batasan pertidaksamaan linear dalam bentuk himpunan penyelesaian. Himpunan terdiri atas titik pada diagram cartesius yang mana apabila koordinat tersebut disubstitusikan pada fungsi linear, maka akan memenuhi syarat yang sudah ditentukan tadi.
Untuk menentukan nilai optimum fungsi objektif, maka kamu bisa menggunakan metode grafik. Cara selengkapnya adalah sebagai berikut :
- Pertama, kamu gambar himpunan penyelesaian pada diagram cartesius.
- Setelah itu, tentukan titik ekstrem dari perpotongan garis batas satu sama lain. Titik ekstrem ini ialah bukan hanya berupa himpunan penyelesaian dari batasan namun juga memiliki kemungkinan agar fungsi jadi optimum.
- Jika sudah, kamu tinggal menyelidiki nilai tersebut menggunakan garis selidik maupun membandingkan nilai-nilainya di setiap titik ekstrem.
Ketika kamu memilih memakai garis selidik, maka adakan diperoleh fungsi ax + by, maka garis selidiknya menjadi ax + by = Z. Nilai z ini bisa menggunakan nilai sembarang. Garis akan dibuat sesudah grafik dibuat. Garis ini dibuat pada area himpunan penyelesaian awal. Lalu, buat lah garis yang sejajar dengan garis selidik yang sudah dibuat.
Pedoman agar kamu lebih mudah menyelidiki nilai fungsi optimum adalah :
- Syarat a > 0
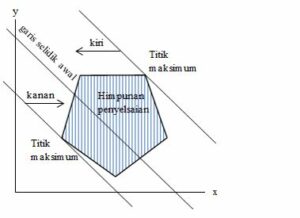
Apabila maksimum, maka harus dibuat gari sejajar dengan garis selidik di awalnya. Kamu pun akan membuat himpunan penyelesaian yang ada pada bagian kiri garis. Titik maksimumnya adalah titik yang dilalui oleh garis itu.
Sedangkan apabila minimum, maka akan disusun garis yang sejajar dengan garis selidik awal dan himpunan penyelesaiannya ada pada bagian kanan garis. Titik minimumnya adalah yang dilalui oleh garis itu.
Kamu bisa melihatnya dengan jelas pada gambar berikut :
- Syarat b > 0
Jika maksimum, buatlah himpunan penyelesaian pada bawah garis dengan garis sejajar garis selidik. Titik maksimum adalah yang dilalui oleh garis.
Sedangkan jika minimum, maka kamu perlu membuat garis sejajar dengan garis selidik. Himpunan penyelesaian ada di atas garis itu. Titik minimumnya adalah yang dilalui garis.
Jelasnya, bisa kamu lihat di bawah ini:
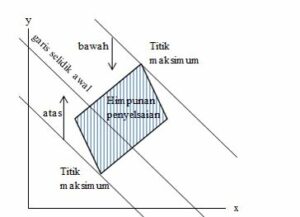
Jika nilai a < 0 serta b < 0, maka akan berlaku kebalikan dari uraian tersebut.
Untuk menyelidiki nilai optimum dari fungsi objektif, kamu juga bisa menggunakan cara berikut. Tentukan titik potong dari garis batas. Titik potong ini adalah nilai ekstrem yang memiliki potensi punya nilai maksimum pada salah satu titiknya. Lalu, dari titik ini akan ditentukan nilai setiap fungsi, lalu kamu bandingkan. Nilai terbesar adalah nilai maksimum serta nilai terkecilnya adalah nilai minimum.
Contoh Soal Program Linear dan Pembahasannya
Tidak lengkap rasanya pembahasan program linear tanpa mengakhirinya dengan contoh soal program linear dan penyelesaiannya. Tak perlu berlama-lama, ini dia contohnya!
1. Contoh Soal Program Linear dan Jawabannya
Persamaan x + y = 10 akan diberikan fungsi berupa {(x,y)| x > 0; y > 0; 2x + 3y < 8; 3x + 2y < a}. Tentukan nilai a yang terdapat di fungsi tersebut sehingga mendapatkan nilai maksimum x + y = 10!
Jawab :
Kamu perlu menulis semua fungsi yang ada di soal, yakni :
x > 0
y > 0
2x + 3y < 8
3x + 2y < a
Lalu, kamu jumlahkan dua fungsi tersebut dengan cara :
2x + 3y < 8
3x + 2y < a +
5x + 5y < 8 + a
Kemudian, buat lah bentuk yang berbeda, yakni menjadi :
5 (x + y) < 8 + a
Lalu, menjadi :
5 (x + y) < 8 + a
5 (10) < 8 + a
50 – 8 < a
42 < a
Untuk bisa memeroleh nilai maksimum x + y = 10, maka, nilai a > 42
2. Contoh Soal Program Linear dan Jawabannya
Petani jeruk sedang memanen hasil jeruknya tahun ini. Petani tersebut menyewa 30 truk dan colt yang mempunyai total muatan 300 karung. Setiap truk bisa menampung maksimal 15 karung dan mobil colt hanya bisa mengangkut 10 karung saja. Tentukan model matematika dari ilustrasi tersebut! Dimisalkan truk adalah x dan colt adalah y, maka fungsinya menjadi :
15x + 10y = 300
3x + 2y = 60
x + y = 30
Itulah pembahasan mengenai program linear. Semoga ulasannya mudah dipahami, ya! Sebab, materi program linear ini kerap digunakan untuk berbagai kegiatan, seperti untuk mengoptimalisasi penjualan.
Pastikan kamu juga mengoleksi model soal program linear yang lain supaya semakin bertambah kemampuannya. Semoga bermanfaat!