Suku Banyak – Tentunya, kamu sudah paham dengan istilah persamaan kuadrat, kan? Untuk menentukan unsur persamaan kuadrat tersebut, kamu bisa melakukan kuadrat sempurna, pemfaktoran, dan sebagainya. Namun, bagaimana caranya kamu bisa menentukan suku persamaan dengan pangkat lebih dari 2? Nah, kali ini, kamu akan mempelajari tentang sistem persamaan tersebut dalam materi polynomial atau suku banyak.
Nantinya, kamu akan belajar tentang berbagai metode untuk menentukan suku pada persamaan suku banyak. Seperti dengan metode substitusi, horner, dan sebagainya. Wah, excited sekali, ya! Kalau begitu, langsung saja masuk ke materinya!
Pengertian Suku Banyak
Suku banyak sendiri bisa kamu artikan sebagai bentuk aljabar yang terdiri atas konstanta, variabel, dan juga eksponen. Bentuk umum dari persamaan suku banyak adalah anxn, an-1xn-1, an-2xn-2, dan seterusnya. Dari bentuk tersebut, kamu bisa lihat kalau suku itu ada variabel, koefisien, dan juga konstantanya.
Kamu juga bisa tahu kalau urutan suku banyak dimulai dari suku yang mempunyai pangkat paling tinggi. Pada bentuk tadi, pangkat tertingginya adalah anxn. Baru kemudian diikuti dengan suku yang mempunyai pangkat semakin menurun. Lalu, diakhiri dengan suku berpangkat nol. (a0).
Pangkat tertinggi pada suku banyak bisa disebut sebagai ‘derajat’, serta hanya terdapat pada satu variabel saja. Berdasar pada bentuk umum tadi, derajatnya adalah n. Nah, for your information, suku banyak bisa saja punya variabel lebih dari satu. Variabelnya juga bisa memakai huruf x, y, dan sebagainya.
Contoh Suku Banyak
Untuk lebih paham tentang suku banyak, kamu bisa cek contohnya langsung.
Salah satu contoh suku banyak bisa kamu lihat di bawah ini, ya!
8y3 – 20y2 – 17y – 10
Jadi, bisa kamu lihat kalau contoh tersebut punya suku, sedangkan derajat suku banyaknya adalah 3.
Ada juga contoh lainnya, yaitu:
6xy3 + 2xy2 – 15y – 5
Pada contoh tersebut juga ada 4 suku, sedangkan variabelnya adalah x dan y, koefisiennya adalah 6, 2, dan juga -15. Konstanta pada contoh itu hanya -5, sedangkan eksponennya adalah 2 yaitu pada y2 dan 3 pada y3.
Nah, sudah paham kan?
Nantinya, setiap suku akan digabung dengan operasi baik pengurangan atau penjumlahan. Namun, kamu harus perhatikan beberapa hal berikut ini!
- Variabel tidak bisa membagi suku banyak.
- Pangkat atau eksponen pada suku banyak harus berupa bilangan cacah (0, 1, 2, 3, dan seterusnya).
- Bukan suku tak terbatas.
Nilai Suku Banyak
Bentuk fungsi suku banyak yang umum diketahui adalah:
f (x) = anxn + an-1xn-1 + an-2xn-2 + … + a2x2 + a1x + a0
Selain f(x), biasanya, fungsi suku banyak juga dapat dinyatakan menggunakan simbol S(x) atau P(x). Untuk mencari nilai dari suku banyak, kamu juga bisa menggunakan cara substitusi maupun horner. Yuk, bahas satu per satu!
Substitusi
Cara substitusi dilakukan dengan mengganti variabel x menggunakan bilangan tertentu yang sudah diketahui. Sebagai contoh, kamu bisa melihat soal berikut!
- Tentukan nilai dari suku banyak berikut jika x = -1, f (x) = 4x3 + 6x2 – 5x + 20.
Jawab:
f (x) = = 4x3 + 6x2 – 5x + 20, lalu, kamu masukkan nilai -1 pada setiap x.
f (-1) = 7 (-1)3 + 6 (-1)2 – 5 (-1) + 20
f (-1) = -7 + 6 + 5 + 20 = 24
Jadi, nilai dari f (x) = 4x3 + 6x2 – 5x + 20 dengan x = -1 adalah 24.
Gampang banget, ya? Kamu hanya perlu lebih teliti saat memasukkan angka tersebut.
Horner
Cara horner juga cukup mudah, kok! Kamu hanya perlu melakukan beberapa langkah berikut ini! Biar gampang, kita buat suatu permisalan, ya!
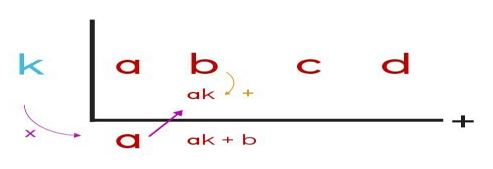
Semisal, fungsi suku banyak diketahui P(x) = ax3 + bx2 + cx + d, dengan x = k.
Lalu, kamu perlu melakukan langkah pertama yakni dengan menulis semua koefisien yang terdapat dalam suku banyak di atas berurutan. Kamu harus memulainya dari suku yang punya pangkat tertinggi hingga yang paling rendah.

Apabila salah satu suku tidak ada, kamu tulis saja dengan angka nol. Seperti pada P(x) = ax3 + cx + d. Kamu perlu menuliskan variabel dengan pangkat 3, 1, serta nol karena tidak terdapat pangkat 2. Sehingga, pada penulisannya, koefisien pangkat 2 tetap harus kamu tulis, tapi diisi menggunakan angka nol.

Langkah kedua, kamu tulis nilai x = k yang sudah diketahui pada sisi yang paling kiri.

Langkah ketiga, isi lah daerah hasil pada baris yang ke tiga kolom pertama menggunakan koefisien awal.

Langkah keempat, kamu kalikan hasil dari langkah ketiga tadi dengan k. Kemudian, letakkan hasilnya pada baris kedua pada kolom kedua.

Langkah yang kelima adalah dengan menjumlahkan koefisien kedua pada baris yang pertama dengan baris yang kedua. Kemudian, kamu letakkan hasilnya di baris yang ketiga.
Kamu ulangi lagi langkah sebelumnya hingga hasil akhirnya bisa diketahui seperti ini:

Gimana? Masih bingung? Tidak apa-apa, kalau sudah membahas contoh soal di bawah ini, kamu akan lebih paham, kok!
Contoh Soal
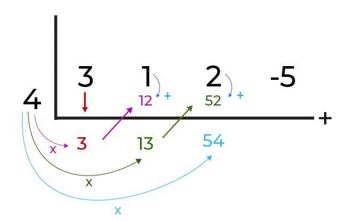
Hitung nilai suku banyak g (x) = 3x3 + x2 + 2x – 5 untuk x = 4
Jawab:
Kamu tulis dulu semua koefisiennya di baris pertama. Kamu tulis secara urut mulai dari koefisien suku yang memiliki pangkat paling tinggi, yaitu 3 hingga yang paling rendah, yaitu -5.
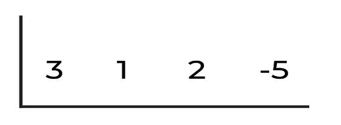
Kemudian, tulis lah nilai x pada sisi yang paling kiri, lalu, tulis koefisien dari suku yang pertama yakni 3 pada baris yang ketiga (daerah hasil).
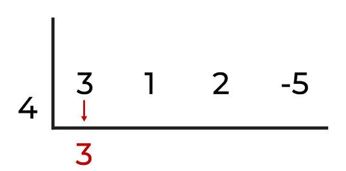
Kalikan angka dengan hasil yang sudah kamu peroleh dari langkah kedua, yaitu 3, kemudian, letakkan hasil di kolom yang ke 2 baris 2.

Lalu, kamu jumlahkan angka 1 dengan 12 sehingga hasilnya menjadi 13. Lalu, kalikan lagi angka 4 dengan 13, hasilnya 52 diletakkan di baris ke 2 dan kolom yang ke 3. Kamu bisa lihat di bawah ini!
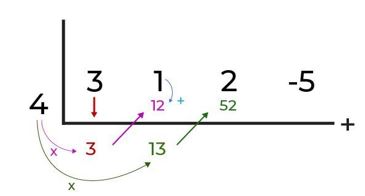
Kamu lanjutkan step sebelumnya dengan menjumlahkan koefisien pada suku selanjutnya dan letakkan pada baris yang selanjutnya. Lihat gambar di bawah ini!
Dan yang terakhir, kamu kalikan lagi angka 4 dengan 54, sehingga menghasilkan angka 216. Kamu letakkan hasilnya pada baris yang ke 2 dan kolom 4. Lalu, suku yang terakhir dijumlahkan dengan angka 216. Lalu, hasilnya menjadi 211.
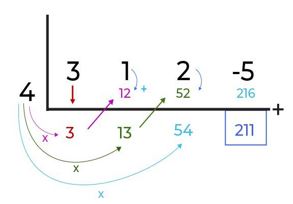
Sehingga, bisa diperoleh suku banyak g(x) = 3x3 + x2 + 2x – 5 dengan x = 4, hasilnya adalah 211.
Menurut kamu, mana metode yang paling gampang? Sebetulnya, keduanya sama-sama gampang asalkan kamu bisa lebih teliti saat mengoperasikannya.
Mau terima challenge? Baik lah, silakan kamu kerjakan soal berikut ini, lalu, kerjakan di buku tulismu! Siap, ya!
Tentukan nilai dari suku banyak berikut ini!
- f (x) = x3 – x + 1 dengan x = 1/3
Pastikan kamu mengerjakan soal tersebut dengan dua metode yang sudah dijelaskan tadi, ya! Atau kamu bisa pilih salah satu metode yang paling mudah dan simpel. Selamat mencoba!

