Apakah Kamu merupakan seorang yang gemar dengan fisika? Apabila iya mungkin Kamu sudah tidak asing lagi dengan istilah kesetimbangan benda tegar. Kesetimbangan yang dimaksud di sini adalah sebuah kondisi ketika momentum pada benda tegar akan memiliki nilai nol.
Hal tersebut berarti bahwa apabila benda yang awalnya diam, maka benda akan tetap diam. Akan tetapi apabila pada awalnya benda berada dalam kondisi bergerak maka benda akan tetap bergerak dengan kecepatan yang konstan. Untuk lebih meningkatkan pemahaman Kamu terkait materi ini, maka simak uraian berikut.
Pengertian Kesetimbangan Benda Tegar
Sebuah istilah yang terdapat pada ilmu fisika yang dapat dimanfaatkan untuk menyatakan suatu kondisi yang mana momen sebuah benda akan selalu sama dengan nol maka disebut dengan istilah kesetimbangan benda tegar. Selain itu dapat diartikan pula sebagai torsi pada sebuah sumbu yang diakibatkan oleh adanya gaya.
Syarat dari Kesetimbangan Benda Tegar
Hukum newton II merupakan salah satu hukum dalam fisika yang menjadi syarat dari terjadinya kesetimbangan. Hukum ini menyebutkan bahwa apabila terdapat resultan gaya, maka pada benda tersebut dapat dianggap sebagai jenis partikel yang mana nilainya sama dengan nol sehingga benda dapat bergerak dengan arah resultan benda sama dengan arah gerak benda.
Sehingga syarat dari terjadinya kesetimbangan benda yaitu ketika benda tersebut telah diletakkan pada posisi yang sama maka Kamu dapat mengetahui bahwa benda tersebut tidak mengalami gerak, sedangkan apabila Kamu meletakkan benda pada posisi miring sehingga benda tersebut dapat bergerak. Sebab disesuaikan dengan kemiringan dari benda yang diinginkan.
Contohnya kamu memiliki bola, papan datar, serta sebuah benda dengan bentuk segitiga. Nah Kamu dapat meletakkan papan pada salah satu titik ujung pada benda segitiga tersebut sehingga terjadi suatu kesetimbangan selanjutnya Anda dapat meletakkan bola tersebut sehingga bola akan berhenti. Sedangkan apabila papan digerakkan, maka bola akan bergerak sesuai kemiringan papan.
Rumus Kesetimbangan Benda Tegar
Kesetimbangan benda atau torsi dapat ditulis secara matematis yaitu:
τ =r F sin θ
Dengan keterangan bahwa τ merupakan sebuah torsi, r adalah jarak dari titik tangkap gaya dengan sumbu. Dan θ merupakan sudut lancip dari garis r dengan F.
Syarat dari Kesetimbangan Benda
Apabila keadaan benda memenuhi syarat yang ada di bawah ini maka suatu sistem tersebut dapat dikatakan mengalami kesetimbangan.
1. Dari seluruh gaya yang bekerja pada benda harus bernilai nol, sehingga dapat dikatakan memiliki sebuah vektor.
∑Fx = 0 dan ∑Fy = 0
2. Buatlah sumbu tegak lurus pada sebuah bidang dengan gaya yang seimbang. Lalu ambil patokan di mana apabila torsi yang bisa mengakibatkan putaran memiliki nilai yang positif jika searah jarum jam, serta akan bernilai negatif jika berlawanan dengan arah jarum jam.
∑τ = 0
Jenis-Jenis Kesetimbangan Benda Tegar
Apabila dilihat secara umum, kesetimbangan dari benda tegar dapat dibedakan menjadi dua yaitu sebuah kesetimbangan dinamis atau benda yang sedang bergerak naik dengan cara linear atau translasi maupun dengan cara angular, serta sebuah kesetimbangan statis yang mana benda akan benar-benar berada pada kondisi diam.
1. Kesetimbangan Benda Stabil
Dalam kesetimbangan ini maka terdapat suatu kesetimbangan yang mana pada sebuah benda dipengaruhi oleh adanya gaya, sehingga benda tersebut bisa kembali dalam bentuk semula.
Contohnya yaitu terdapat sebuah kelereng yang terdapat pada wajan penggorengan. Pada kondisi seperti ini kelereng tersebut akan kembali dalam kondisi seperti awalnya saat wajan mendapatkan gaya atau ketika wajan tersebut digoyang-goyangkan ke arah yang bebas.
2. Kesetimbangan Benda Labil
Dalam konsep kesetimbangan benda tegar terdapat konsep lain yang relevan yaitu kesetimbangan benda yang labil. Kesetimbangan labil dapat diartikan sebagai benda yang mana apabila diberi gaya sedikit saja yang berupa gangguan, serta gaya yang berpindah sehingga tidak bisa kembali dalam keadaan awal.
Contohnya adalah terdapat sebuah kelereng yang terletak pada wajan dalam posisi terbalik, sehingga dalam keadaan ini kelereng tersebut akan terjatuh dan akan berpindah apabila terdapat gangguan meskipun hanya sedikit.
3. Kesetimbangan Netral atau Indeferen
Suatu kesetimbangan yang mana akan terjadi pada sebuah benda yang diberikan suatu gangguan sehingga titik berat sebuah benda tidak berubah seringkali disebut dengan kesetimbangan netral atau indeferen. Untuk lebih memudahkan pemahaman dapat Kamu simak contoh berikut:
Pada sebuah kelereng yang mana diberi sebuah gangguan sehingga titik beratnya tidak mengalami perubahan sehingga titik berat dari kelereng akan terus berada pada pusat kelereng.
Penerapan Kesetimbangan Benda Tegar di Kehidupan Sehari-hari
Salah satu materi fisika yang seringkali disepelekan padahal memiliki manfaat yang begitu besar yaitu materi terkait kesetimbangan benda tegar pada sebuah timbangan yaitu neraca ohaus. Konsep yang diterapkan pada neraca ohaus ini memang benar-benar menggunakan konsep kesetimbangan yang mana pada tusa neraca sebelah kanan dapat menimbulkan putaran yang searah dengan jarum jam.
Dengan hal tersebut dapat diartikan bahwa nilai torsi adalah positif, dan pada tuas yang berada pada sebelah kiri akan membuat putaran yang berlawanan dengan arah jarum jam sehingga memiliki nilai torsi negatif.
Sehingga akan diketahui juga bahwa sebuah benda yang berada di sebelah kiri akan membuat posisi yang sama dengan beban yang terdapat pada tuas yang berada di sebelah kanan dan pada tuas yang berada di sebelah kiri.
Contoh Soal Kesetimbangan pada Benda Tegar
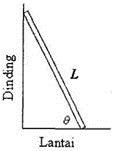
1. Apabila diperhatikan, gambar di atas merupakan sebuah tangga yang homogen dengan panjang sebesar L, tangga tersebut diam dengan bersandar di tembok yang mana tembok tersebut licin pada bagian atas lantai yang kasar dan memiliki koefisien gesek statis antara tangga dengan lantai yaitu µ.
Jawab
Diketahui:
∑Fy berniali 0, maka untuk nilai yang lainnya seperti NL – mg = 0, maka benda akan tetap disebut memiliki nilai rotasi yang baik.
Jawab:
NL L cos θ – fs L sin sin θ – mg L/2 cos θ = 0
NL L cos θ – µ L sin sin θ – mg L/2 cos θ = 0
Kemudian substitusikan NL yang berada di persamaan pertama, sehingga didapatkan hasil
Mg L cos θ – µ mg L sin θ – mg L/2 cos θ = 0
Cos θ – µ sin – ½ cos θ = 0
Cos θ/2 – µ sin θ = 0
Cos θ/2 = µ sin θ
1/2µ = µ sin θ cos θ/2
Tan θ = 1/2µ
2. Pada sebuah batang sepanjang A-B dengan massa diabaikan, kemudian digantung sebuah balok memiliki massa 10 kg. dari ujung A diletakkan balok dengan massa 4 kg dengan jarak 2 m. apabila panjang batang dari ujung A ke B sebesar 6 m, Maka tentukan tegangan tali T.
Jawab:
∑τ = 0
W1 (mAB) + W2 (2) – t sin 30 (AB) = 0
100 (6) + 40 (2) – T (1/2 . 6) = 0
600 + 80 – 3T = 0
3T = 680
T = 600/3
T = 226,6 N