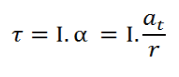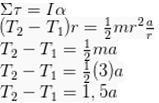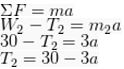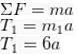Apakah sebelumnya Kamu pernah mempelajari tentang dinamika rotasi? Apabila pernah pasti Kamu sudah tahu dong, nah untuk yang belum tahu tidak perlu khawatir, dalam penjelasan berikut akan diuraikan secara lengkap mulai dari pengertian hingga contoh soalnya.
Benda dapat dikatakan bergerak secara rotasi apabila benda tersebut mengalami pergerakan dan lintasannya berupa lingkaran atau dengan kata lain benda tersebut bergerak tepat pada sumbu putarnya.
Pengertian Dinamika Rotasi
Salah satu cabang ilmu mekanika yang membahas terkait benda yang dapat bergerak dan membutuhkan adanya gaya disebut dengan dinamika rotasi. Apabila seluruh bagian benda mengalami gerak yang mengelilingi poros maupun sumbu putarnya yang berada di salah satu bagian dari benda tersebut, maka benda tersebut dikatakan berotasi.
Sedangkan saat benda mengalami gerak translasi, sebenarnya benda tersebut bisa mendapatkan gaya dari luar yang diberikan pada benda tersebut. Perlu Kamu ketahui juga bahwa arah lintasan benda tersebut juga dapat mengalami perubahan karena terdapat gaya yang diterima.
Akan tetapi lain halnya jika benda mengalami gerak memutar yang berada dalam lintasan melingkar, tentunya benda tersebut juga mendapatkan gaya, namun seringkali dikenal dengan sebutan torsi.
Momen Gaya atau Torsi beserta Rumusnya
Beberapa pengertian terkait momen gaya atau torsi dapat diartikan sebagai berikut:
- Torsi merupakan sebuah gaya yang terjadi pada sumbu putar serta dapat mengakibatkan benda yang dikenai gaya tersebut bisa bergerak secara melingkar maupun berputar.
- Untuk gaya yang dapat mengakibatkan sebuah benda mengalami gerak melingkar maupun berputar dengan arah searah dengan putaran jarum jam (clockwise) maka disebut dengan momen gaya atau torsi dengan nilai positif, sedangkan jika arah gerak benda berlawanan dengan arah putaran jarum jam atau (counterclockwise), maka torsi atau momen gayanya memiliki nilai negatif.
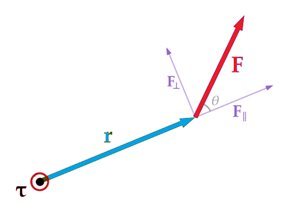
Untuk lebih memudahkan akan pemahaman Kamu, coba perhatikan gambar berikut.
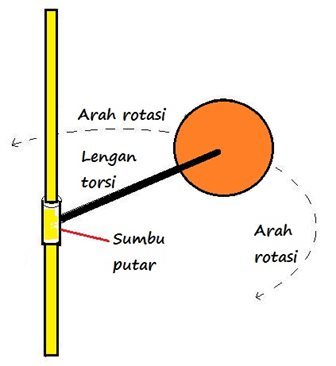
Sehingga torsi ataupun momen gaya bisa dirumuskan secara matematis sebagai berikut:![]()
Dengan keterangan
merupakan momen gaya atau torsi dengan satuan Nm
r merupakan penjang lengan gaya, mempunyai satuan m, dan
F adalah gaya yang diberikan dengan arah gerak lurus dengan lengan gaya, memiliki satuan N
Apabila terdapat sebuah gaya yang bekerja memiliki lengan gaya yang tidak tegak lurus, maka besar memiliki besar torsinya yang dapat dihitung dengan rumus sebagai berikut.
= r × F × sin θ
Yang mana nilai ini merupakan sebuah sudut antara lengan gaya dengan gaya yang bekerja, untuk lebih jelasnya dapat Kamu perhatikan gambar berikut.
Bagaimana Perbedaan antara Gerak Translasi dan Gerak Rotasi?
Setiap benda pasti memiliki potensi untuk dapat bergerak secara translasi atau sering disebut dengan gerak rotasi. Gerak translasi dalam konsep dinamika rotasi merupakan sebuah gerak benda yang memiliki arah lurus atau melengkung.
Pada gerak translasi juga menggunakan konsep dari hukum Newton II. Sedangkan untuk gerak rotasi merupakan gerak suatu benda yang dapat berputar pada poros dari benda tertentu. Gerak rotasi yang terjadi diakibatkan oleh karena terdapat torsi. Benda yang mengalami gerak rotasi pasti mengalami suatu torsi.
Lengan Momen
Lengan momen merupakan sebuah sebutan pada benda yang mempunyai jarak dari titik poros rotasi hingga ke gaya yang sifatnya saling tegak lurus. Perlu untuk Kamu ketahui juga bahwa torsi adalah sebuah besaran vektor. Sehingga torsi ini memiliki arah.
Momen Inersia
Selain momen gaya atau torsi, dalam bahasan dinamika rotasi juga terdapat konsep momen inersia yang mana konsep ini pertama kali diberikan oleh seorang ahli dengan nama Leonhard Euler.
Kelembaman pada suatu benda untuk dapat berputar pada porosnya merupakan penjabaran dari momen inersia yang dikatakan pula sebagai bentuk ukuran kesukaran sehingga dapat membuat benda mengalami gerak berputar atau bergerak melingkar. Penting untuk dipahami juga bahwa besar dari momen inersia sangat bergantung pada bentuk serta posisi sumbu putar yang terdapat pada benda.
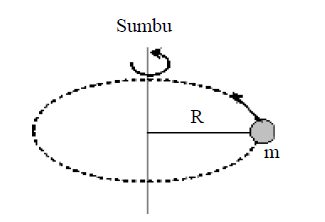
Dari gambar, maka momen inersia bisa dirumuskan secara matematis dengan rumus sebagai berikut:
I = mr2
Yang mana I merupakan momen inersia itu sendiri dengan satuan kgm2, r merupakan jari-jari dengan satuan m, dan m adalah massa suatu partikel atau benda dengan satuan kg.
Sebuah momen inersia akan memiliki hasil yang sama dengan jumlah dari seluruh momem inersia yang menyusunnya apabila benda tersebut memiliki susunan partikel yang lebih kecil. Dapat dirumuskan sebagai berikut.
Dalam bahasan dinamika partikel, penting untuk Kamu ketahui bahwa suatu gaya sebesar F dapat menyebabkan sebuah benda mengalami gerak translasi dengan kecepatan yang linear. Sedangkan untuk suatu torsi juga dapat menyebabkan sebuah benda mengalami gerak rotasi pada suatu poros tertentu.
Oleh karena sebuah torsi dapat dianalogikan sebagai gaya F serta percepatan sudut α dianalogikan dengan dengan percepatan linear a. maka bisa dihasilkan hukum Newton II yaitu sebagai berikut:
Yang mana I merupakan momen inersia dengan satuan kgm2, α merupakan percepatan sudut dengan satuan rad/s2, τ adalah torsi dengan satuan Nm, r adalah jarak titik ke poros dengan benda, memiliki satuan m.
Setelah mengetahui rumus, maka Kamu dapat menghitung energi kinetik dari rotasi suatu massa dengan rumus sebagai berikut:
Contoh Soal Dinamika Rotasi
Setelah membahas materi terkait dinamika rotasi, maka untuk lebih memperdalam pengetahuan, maka akan dilanjutkan dengan contoh soal sebagai berikut:
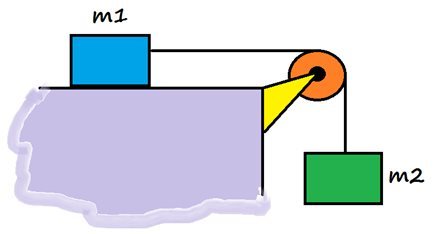
1. Dari gambar, maka bisa Kamu ketahui bahwa terdapat sebuah katrol silinder pejal ( ) yang mempunyai massa 3kg serta memiliki berjari-jari sepanjang 20 cm yang dihubungkan dengan dua buah tali yang terpaut dengan benda lain yang memiliki massa m1 sebesar 6kg serta m2 sebesar 3kg. dengan ketentuan bahwa sistem berada dalam kondisi tertahan dan diam yang kemudian dilepaskan.
Jika tidak terdapat gaya gesek dengan lantai, maka kecepatan kedua benda tersebut adalah?
Diketahui:
Katrol:
Sistem m2 :
Sehingga sistem m1 :
Dengan cara mensubstitusi ketiga persamaan diatas, kita dapat mengetahui besaran nya yaitu:
30 – 3a – 6a = 1,5a
30 – 9a = 1,5a
30 = 10,5a
a = 2,86m/s2
2. Sebuah cakram pejal dengan massa 2 M dan memiliki jari-jari sebesar R, pada bagian tepi cakram dililit dengan tali, yang mana pada bagian salah satu ujungnya diberi beban dengan massa m. saat beban tersebut dilepaskan kembali, maka katrol akan bergerak rotasi dengan percepatan sudut. Apabila pada katrol tersebut ditempel dengan benda yang bermassa M, katrol juga akan bergerak memutar dengan percepatan sudut yang sama, maka massa beban harus…..? I katrol = ½ mr2
Diketahui:
Massa katrol cakram pejal sebesar 2 M
Jari-jari dari katrol cakram pejal sebesar R
Massa bebas sebesar m
Ditanya: berapakan massa beban?
Dijawab: untuk menghitung momen inersia dari katrol cakram pejal, untuk sebelum ataupun sesudah ditempel benda dengan massa M yaitu:
Momen inersia 1
I = ½ mr2
I = ½ (2M) (R)2 = M R2
Momen Inersia 2
I = ½ mr2
I = ½ (2M + M) (R)2
I = ½ (3M) (R)2
I = 1,5 M R2